機械学習におけるパラメータ(重み)最適化手法をまとめる。
本記事の目的は、勾配降下法の基本手法とその派生の最適化手法のメリット・デメリットを理解し、どの場面ではどの手法が適切なのかの判断ができるようになること。
【決定版】スーパーわかりやすい最適化アルゴリズム -損失関数からAdamとニュートン法-
の記事をかなり参考にさせていただいた。この記事の内容を自分の理解に合わせて、割愛・追加している。
以前の記事で、勾配降下法とその代表例である、確率的勾配降下法(SGD)とミニバッチSGDについて触れた。
本記事では、再度この2つの手法に触れ、その発展として開発された5つの手法(モーメンタム、NAG、RMSProp、Adam、ニュートン法)について触れる。
ただ、ここで記載する手法はすべて勾配降下法を基にしていることを明記しておく。
本記事では以下の流れで説明する。
1.1 バッチ勾配法
元祖、最適化手法ってイメージ。すべての手法の原点。
全データを使った最適化手法。2つのデメリットがあるとされている。
- 重みの更新に全データを使うので計算量が多い→並列化で解決できる
- バッチ勾配法は全データに基づくため、更新に揺らぎ(ノイズ)が少なく、局所最小値から抜け出しづらい傾向がある
1.2 確率的勾配降下法(SGD)
バッチ勾配法よりも局所最小値から抜け出しやすい方法。ランダムに1つのデータを選びパラメータ(重みとバイアス)の更新に使うことで、パラメータが大きく更新され、局所最小値から抜け出すことができる。
デメリットとして、1つのデータを使うため最適化のプロセスを並列化できないことが挙げられる。
1.3 ミニバッチSGD
16個や32個などの小さいデータの塊を使ってパラメータを更新する。これにより並列処理が可能になり、SGDよりも早く最小値に到達できる。ハードウェアの進化により、現在の機械学習ではほぼ確でSGDよりもミニバッチ処理が使われる。
しかしミニバッチSGDにもまだ高速化のポテンシャルが残されている。ミニバッチSGDでは、Pathological Curvatureと呼ばれるところに陥った際、パラメータが振動してしまい、学習のスピードが遅くなってしまう。Pathological Curvatureとは谷間のように狭く曲がった領域で、x方向には急に変化して、y方向にはなだらかに変化する場所である。
2.1 モーメンタム法
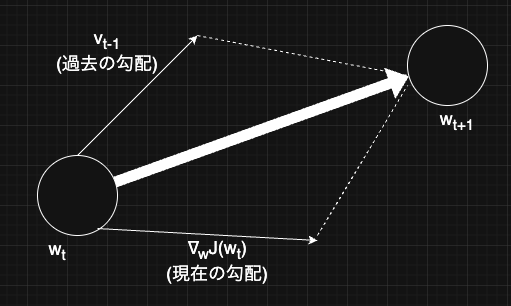
ミニバッチSGDにおける振動問題を解決する手法として、考案されたのがまず最初に紹介するモーメンタム法。物理学で使われる運動量(モーメンタム)の概念を借りていて、勾配に基づくパラメータの更新に、過去の更新方向を加味することで、振動を抑制する。動いているものはその方向に動き続けたいという慣性の概念を利用している。
$$
v_t = \beta v_{t-1} + (1 – \beta) \nabla_w \mathcal{L}(w_t)
$$
$$
w_{t+1} = w_{t} – \eta v_t
$$
ここで、$v_t$は更新の累積的な速度(モーメンタム)、$\nabla_w \mathcal{L}(w_t)$は現在の勾配、$\eta$は学習率、$\beta$はモーメンタム係数(0
すなわち、上述の更新式をベクトル図で表すと、これまでの更新の累積と現在の勾配の和を用いて、パラメータを更新していることがわかる。
2.1.1 移動平均
なぜ過去の更新方向を考慮すると振動が抑制されるのか。移動平均の概念を理解するとこの謎が理解できる。
移動平均とは、データのノイズ(短期的な変動)を減らし、トレンド(長期的な動き)を強調するもの。すなわち、移動平均は急な変化に動じないという特徴を持つ。
ここで、移動平均の式は以下のように表される。
$$
v_t = \beta v_{t-1} + (1 – \beta)G
$$
$v_{t-1}$は全時刻での移動平均後の値、$G$は現時刻の値
モーメンタム法の式と見比べると、実はモーメンタム法は単縦に勾配を移動平均しているだけだとわかる。移動平均は急な変化に動じないという特徴を持つ、すなわち振動のような急激な変化に対しても動じずに安定して、パラメータの更新を可能にする。
import numpy as np
import matplotlib.pyplot as plt
# データ生成 (急激な変化を含む)
np.random.seed(42)
n = 100
G = np.random.randn(n) * 10 # 現時刻の勾配 (ランダムで急激な変化が含まれる)
# 移動平均のパラメータ
beta = 0.9
# 移動平均を計算
v = np.zeros(n)
for t in range(1, n):
v[t] = beta * v[t-1] + (1 - beta) * G[t]
# グラフの作成
plt.figure(figsize=(10, 6))
plt.plot(G, label="Original Data with Rapid Change")
plt.plot(v, label="Moving Average", linewidth=2)
plt.xlabel("time")
plt.ylabel("value")
plt.legend()
plt.grid(True)
plt.show()
移動平均のグラフ
生成されたデータは平均0、標準偏差1の一様分布を持つ。移動平均のグラフは急激な変化に動じず、この元データの性質をキャプチャーできていることがわかる。
2.1.2 NAG (Nesterov Accelerated Gradient)
モーメンタム法では、慣性(過去の勾配の方向に動き続けたい性質)のようなものを現在の勾配に付け加えることにより、より滑らかなパラメータ更新を目指している。しかし、そもそもこの慣性の方向が正しい方向(つまり損失を減らす方向)を向いているとは限らない。
そこで、この慣性の方向が正しい方向であることを少しでも保証しようよ、というのがNesterov(ネステロフ)の加速勾配法(NAG)である。
数式で書くと、
$$
v_t = \beta v_{t-1} + (1 – \beta) \nabla_w \mathcal{L}(w_t – \beta v_{t-1})
$$
$$
w_{t+1} = w_{t} – \eta v_t
$$
もう一度、モーメンタム法の式と比べると
$$
v_t = \beta v_{t-1} + (1 – \beta) \nabla_w \mathcal{L}(w_t)
$$
$$
w_{t+1} = w_{t} – \eta v_t
$$
以上から、NAGは更新する位置を一歩先に予測し、その予測位置で勾配を計算している。
未来を予測しているから、慣性項は$w_{t+1} – \beta v_{t}$なのではと思ったけど、これは間違い。なぜなら、今の時点で、$w_{t+1}$の値はわからないから。未来の値を考慮すると言ったが、未来の重みの値は現在の時点では分からないので使えない。
代わりに、これまでの慣性と現在の重みの向きを使って、次の重みの位置を予測する。そして、予測した次の位置で勾配を評価している。これがNAGの本質。
2.2 RMSProp(Root Mean Square Propagation)
学習を安定させるために開発された。モーメンタム法とは別のアプローチでSGDを使った時に発生しがちな以下の問題の解決を図った。
・勾配のスケール(大きさ)が不均一なせいで、一部のパラメータだけ異常に振動する
・逆に更新が遅すぎたりする
これは、各パラメータのスケールが違うことに起因する問題である。例えば、$w_1$は非常に急な方向(勾配が大きい方向)に伸びていて$w_2$はなだらかな方向(勾配が小さい方向)に伸びているといった状態。
つまり関数の状態そのものが原因で、あるパラメータは振動する一方、別のパラメータは停滞するといった状態に陥ることがある。
すなわち、勾配の大きさそのものがパラメータによって違うので、適切な学習率をそれぞれのパラメータごとに適用せず、全部同じ学習率で動かすので不安定になる。
RMSPropは主にこの問題を解決するために開発された。RMSPropは
・勾配が大きいパラメータは小さく更新(学習率を大きく)して
・勾配が小さいパラメータは大きく更新する
以上により、全体として、よりスムーズな最適化をする。
$$
s_t = \beta s_{t-1} + (1 – \beta) (\nabla_w \mathcal{L}(w_t))^2
$$
$$
w_{t+1} = w_{t} – \frac{\alpha}{\sqrt{s_{t} + \epsilon}}\nabla_w \mathcal{L}(w_t)
$$
$s_t$は$w_t$の勾配の二乗の指数移動平均、$\alpha$は学習率、$\epsilon$は分母が0になるのを防ぐための非常に小さな数字を表している。
これにより、勾配が大きい時($\nabla_w \mathcal{L}(w_t)$)は勾配を小さく更新し、勾配が小さいときは勾配の更新は大きくなる。
しかし、RMSPropは局所最小値付近、すなわち勾配が非常に小さい点では移動量も小さくなってしまうため、局所最小値からの脱出は期待できない手法である。
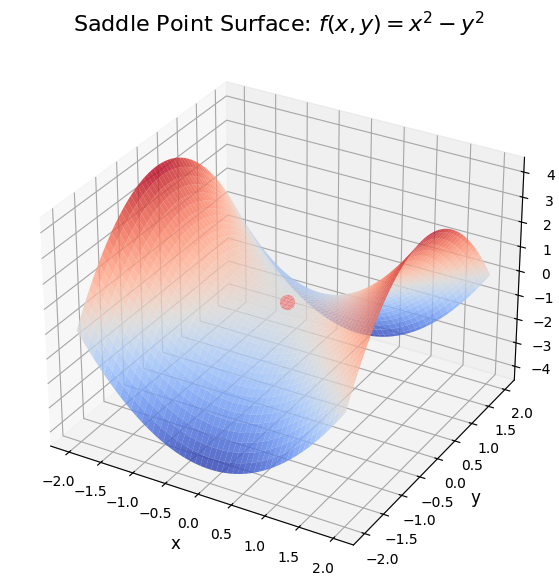
一方、RMSPropは鞍点からの脱出が得意である。鞍点とは、あるパラメータの極大値かつ別のパラメータの極小値であるような点。そのため、普通のSGDでは動きが遅くなって抜け出せなくなる。RMSpropなら、勾配が小さいほうの更新は抑えて、勾配が大きい方は適度に更新することができるので、無駄な振動を抑えて鞍点を早く抜け出せる。
深層学習のようなパラメータの数が多い場合には、局所最小値よりもむしろ鞍点に引っかかるリスクの方が高いため、RMSPropは有用な手法である。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 鞍点を表す関数 (典型的には f(x, y) = x^2 - y^2)
def saddle_point(x, y):
return x**2 - y**2
# グリッドデータを作成
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = saddle_point(X, Y)
# プロット
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='coolwarm', alpha=0.8)
ax.set_title("Saddle Point Surface: $f(x, y) = x^2 - y^2$", fontsize=16)
ax.set_xlabel('x', fontsize=12)
ax.set_ylabel('y', fontsize=12)
ax.set_zlabel('f(x, y)', fontsize=12)
# 鞍点の位置にドットを追加
ax.scatter(0, 0, saddle_point(0, 0), color='r', s=100, label="Saddle Point (0, 0)")
plt.show()
この鞍点は、xの極大値だが、yの極小値
Adamはディープラーニングでデフォルトスタンダード的に使われている超定番の手法。この手法はRMSpropとモーメンタム法の良いとこどり。移動平均で振動を抑制するモーメンタム法と学習率を調整して振動を抑制するRMSPropを組み合わせているだけの手法。
$$
v_t = \beta_1 v_{t-1} + (1 – \beta_1) \nabla_w \mathcal{L}(w_t)
$$
$$
s_t = \beta_2 s_{t-1} + (1 – \beta_2) (\nabla_w \mathcal{L}(w_t))^2
$$
$$
w_{t+1} = w_t – {\alpha}\frac{v_t}{\sqrt{s_t + \epsilon}}
$$
第1式はモーメンタム法の式であり、第2式はRMSPropの式である。第3式はそれらを組み合わせているだけだ。
局所最小値に強いモーメンタム法と、鞍点に強いRMSPropを組み合わせた手法なので、Adamは局所最小値にも鞍点にも強い特性を持ち、効率的かつ安定的にパラメータを更新することができる。
これまでの手法は最急降下法ベースの手法であった。すなわち、損失関数を微分して損失関数を減らす方向に少しずつパラメータを更新する手法であった。
これに対して、損失関数の2階微分を使った最適化手法にニュートン法がある。
$$
w_{t+1} = w_t – \alpha H_{\mathcal{L}}(w_t)^{-1} \nabla \mathcal{L}(w_t)
$$
ここで、各変数は次のように定義されます:
- $w_t$ : 現在のパラメータ(時刻$t$のパラメータ)
- $\alpha$ : 学習率(スカラー値)
- $H_{\mathcal{L}}(w_t)$: 損失関数$\mathcal{L}(w)$のヘッセ行列(二階導関数の行列)
- $\nabla \mathcal{L}(w_t)$: 損失関数$\mathcal{L}(w)$の勾配(一階導関数)
ヘッセ行列は関数の曲率(曲線が上に凸か下に凸かの情報)を表す。ニュートン法ではこの曲率情報を使用してパラメータを更新することで、勾配降下法と比べてより直感的かつ効率的な更新が行える。
しかし、ニュートン法はヘッセ行列の計算とヘッセ行列の逆行列の計算コストが膨大になるため、実務ではほぼ使われることはない。
| 手法 | メリット | デメリット |
|---|---|---|
| バッチ勾配法 | ・理論解析が容易 ・安定して収束する |
・全データを使用するので計算コスト大 ・局所最小値にハマると抜け出しにくい |
| 確率的勾配降下法(SGD) | ・局所最小値から脱出できる可能性あり ・計算量が少ない(1データごと) |
・収束が不安定(ノイズ大)
・並列処理ができない |
| ミニバッチSGD | ・並列化可能で高速 ・SGDより安定した更新 |
・局所最小値で振動して収束が遅くなる場合がある |
| モーメンタム法 | ・振動を抑制し、収束を加速 ・局所最小値を越えやすい |
・モーメンタム方向が悪いと悪影響 |
| NAG | ・モーメンタム法よりも精密な更新が可能 ・未来予測により学習効率が向上 |
・実装が少し複雑 |
| RMSProp | ・学習率の自動調整で収束が安定 ・局所的な最適な学習率設定が可能 |
・ハイパーパラメータ調整(特に減衰率)が必要 |
| Adam | ・モーメンタム+RMSPropのいいとこ取り ・ほぼチューニングなしで安定学習が可能・収束が速い |
・過学習しやすい場合がある ・理論的には一部タスクでSGDに劣る場合もある |
| ニュートン法 | ・収束速度が非常に速い(理想的には) | ・ヘッセ行列(2階微分)の計算コストが莫大・実用上は非現実的 |
5.1 実務上のアドバイス
・まず Adam。よほどの事情がなければAdamで十分。
・もし汎化性能や最終精度にこだわりたいなら、モーメンタム法を使う。
・超巨大モデル・長時間学習を考慮するなら、前半はAdam、後半はニュートン法の切り替え戦略も検討。
・RMSProp・純粋SGD・ニュートン法は、基本的に今の標準環境では選ばない。
ヘッセ行列(Hessian matrix)は、スカラー値aの関数の二階導関数をまとめた行列。ある関数$f(w)$のヘッセ行列は、各パラメータ$w_i$に対して次のように求められる。
$$
H_f(x, y) = \begin{bmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
\end{bmatrix}
$$
さらに、ヘッセ行列から以下のことがわかる
・正定値: すべての固有値が正であるとき、関数はその点で下に凸で、最小値を取る。
・負定値: すべての固有値が負であるとき、関数はその点で上に凸で、最大値を取る。
・不定: 固有値に正と負が混在する場合、その点は鞍点であり、最小値でも最大値でもない。
Views: 0