スマホ向けのミニWebゲームを作りました。
※ 音が出るので注意!!
このゲームはルールベースの自立駆動型エージェントを実装しており、タコとイカがマップ上を適当に彷徨い、敵を追いかけ回し、敵を攻撃して、HPや武器が減ったらアイテムを取りに行ったりします。いわゆる古典的なゲームAIを実装したゲームになります。
作った経緯については以下を参照ください。
2Dゲームの開発はゲームプログラミングの勉強に最適だと思っています。素材の準備もやりやすく、開発時に使うPCのモニターは2次元しか投影できないので、2次元座標だと直感的でわかりやすいです。現在ゲーム開発をするにはUnityやUnreal Engineといった本格的なゲームエンジンを使う開発が主流なのですが、2Dのちょっとしたゲームを作るには不要な機能も多く、エディタも重くて自分にはtoo muchだと思うこともあります。
そこでPhaserやPyxelやEbitengineと言った2Dに特化した軽いフレームワークを使うのも選択肢になってきます。しかしブロック崩しなどの入門書に載っているゲームは作れるようになっても、NPCと対戦するようなさらに難易度の高いゲームはそもそもどう作るのかわからないという方も多いのではないでしょうか。UnityなどのゲームエンジンにはナビゲーションメッシュなどのNPCを動かす機能はあるのでそれをうまく使えばいいのですが、2D特化の軽いフレームワークの場合は基本的にはそこまで機能は備えてないので自分で実装しなければなりません。もちろんゲームをヒットさせる上ではそのような複雑なゲームロジックは必ずしも必要ないのですが、やりたいことが実現できない歯痒さは抱えたままになってしまいます。
オライリーから出ている「実例で学ぶゲームAIプログラミング」はゲームで実現できることの幅を広げてくれる名著です。サンプルコード付きでゲームAIの実践的な書籍として唯一無二の存在です。しかし、原著は2004年の発行で2025年の現時点でサンプルコードが配布されてるリンクが無効になって手に入れられなかったり、サンプルコードを手に入れても動かすにはWindowsで古いDirectXが必要だったり、今からこの本を買って学ぶのはハードルが高いです。他にもゲームAIプログラミングを解説した書籍は存在するのですが、これほどまでに実践的な書籍は見当たりません。ゲームAIと銘打っていますが、ゲームプログラミングの学習にとても役に立ち、その後の私の人生に多大なプラスの影響をもたらしてくれました。私の中では原点にして頂点の技術書です。
私は10年ほど前にこの書籍とサンプルコードを見ながら一通り勉強しました。その後スマホゲーム開発の職についたものの、程なくしてゲーム開発から離れてしまい、久しくゲームプログラミングとは無縁の生活を送っておりました。ただ、当時この書籍で勉強した時の衝撃と具体的な実装方法が未だに頭の片隅に焼きついたままずっと残っていて、どこかのいいタイミングで自分の腕が落ちていないか確かめてみようと思っていました。
イカタコ戦争はPhaserというゲームフレームワークを使ってTypeScriptで書かれています。Phaserにはゲームループの管理やレンダリングなどのゲームの基本機能のみ役割を持たせて、経路探索や衝突判定などの核心的なゲームロジックは自前で実装しています。一般的な内容ではあるのですがこのゲームロジックをざっくり解説いたします。興味があれば参考にしてみてください。
目次
- ゲームループ
- 力と加速度
- マップ
- 経路探索
- ビヘイビアツリー
- 評価関数
- センサーメモリ
- 空間分割
ゲームループ
ゲームプログラミングではゲームループという概念が存在します。ゲームの実装では
- ボタンの入力などのイベントを観測する
- 位置変化や当たり判定などのゲームロジックを計算する
- オブジェクトを出現、消滅させたり位置を少し変えたりする
- GPUに描画コマンドを送信する
という処理を無限ループ内でひたすら繰り返します。この処理のループをゲームループと呼びます。
while(true){
observe();
calculate();
transform();
render();
}
一秒間のうちに何回画面を描き換えるかをフレームレートと呼び、例えばフレームレートが60FPSであれば1秒間に60回画面を描き換えることになり、0.0166秒以内にこのゲームループの処理を終える必要があります。一部のロジックは毎フレーム計算しないとか、レンダリングでGPUに描画コマンドを発行する処理は別スレッドで処理するなど、CPUリソースを分散させてフレームレートを維持します。ゲームプログラミングは処理を早く終わらせるために計算量を減らす工夫が必要です。
力と加速度
移動のロジックには古典物理学の運動方程式を使います。運動方程式は
で表され、これは質量
update(dt: number) {
const F = caluculateForce();
const acceleration = F / m;
const velocity = currentVelocity + acceleration * dt;
clamp(velocity);
const position = currentPosition + velocity * dt;
setPosition(position);
}
update関数は先ほど説明したゲームループで繰り返し呼ばれます。引数dtは前回呼ばれたupdateからの経過時間が渡され、60FPSであれば0.0166秒が渡ってきます。加速度に時間の変化量をかけると速度の変化量になり、速度に時間の変化量をかけると位置の変化量になります。このことから物体に加わる力と物体の現在の速度と位置がわかっていれば、物体の次の位置が計算できます。実装イメージを見ていきましょう。
- タコやイカに加える力を計算します。この力は2次元ベクトルで表現されます。タコやイカに加わる力は①物体が目的地に移動するための駆動力、②壁抜けを防ぐための壁からの反力、③他のタコやイカにめり込まないようにする反力の3つが存在します。それぞれ物体の位置関係で発生する力が計算され、優先順位に基づいて最終的に物体に加えられる力が計算されます。例えば壁に近ければ壁からの反力が大きくなりますが、壁抜けはできないので駆動力より壁からの反力の方が優先度が高くなり、壁からの反力の影響が大きくなります。
- 力がもとまると、運動方程式に従い加速度を求めます。ちなみに質量mのようなパラメータは実際にゲームを動かしながらいい感じになる値を見つけていきます。
- 新しい速度を求めます。速度も2次元ベクトルで表現されます。加速度に時間の変化量をかけて速度の変化量を求め、さらにそれを現在の速度と足し合わせると新しい速度が計算できます。
- 3で求めた速度が最大速度を超えないように調整します。
- 新しい位置を求めます。位置も2次元ベクトルで表現されます。速度に時間の変化量をかけて位置の変化量を求め、さらにそれを現在の位置と足し合わせると新しい位置がもとまります。
- 新しい位置に設定すれば移動は完了です。
実際には力から位置を計算する過程で任意のパラメータを計算に入れ、実際にゲームを動かしながらいい感じになるようにパラメータを細かく調整していきます。ゲームプログラミングにおいてこのようなパラメータはたくさん存在するので、どのようなパラメータなのか分かりやすくなるように管理しておきましょう。
マップ
イカタコ戦争では5種類のマップがあり、ランダムで使用するマップが選択されます。マップはあらかじめ作成し、静的データとして配信されています。jsonで保持するとデータ量があまりに大きくなってしまうので、バイナリファイルにしてzip圧縮することでデータ量を大幅に削減しています。マップには壁とナビゲーショングラフという二つのデータを持っています。それぞれ説明します。
壁

壁は文字通り壁です。物体は壁の外に抜けることはできません。画像では0番から43番までの番号がついた線分で表されています。そして番号が表示されているところから壁とは垂直方向に線が伸びていますが、この線は壁の内側であることを示す法線ベクトルです(実際のゲームでは表示されません)。力と加速度の章でタコやイカは壁に近づくと壁から遠ざかるような力(反力)を受けると説明しましたが、この反力は法線ベクトルの向きに力が発生します。この法線ベクトルがなければどちらが壁の内側になるのかを計算することができません。壁の内側であることを判定するために、この法線ベクトルはさまざまなところで使われています。壁のデータは「壁の始点」と「壁の終点」と「壁の内側を表す法線ベクトル」の3つの2次元ベクトルになります。
ナビゲーショングラフ

ナビゲーショングラフはタコやイカが壁に衝突せずに移動するための移動経路です。その名の通りグラフ構造のためノードとエッジを持ち、エッジをなぞってノード間を移動していくと壁にぶつからずに移動ができます。このナビゲーショングラフはシードフィルアルゴリズムを使って事前に作成しておきます。
シードフィルアルゴリズムを使ってナビゲーショングラフを作成する方法は以下の通りです。
1. シードの設置
まずは壁の中にシードを設置します。シードが壁に近すぎると壁に近い位置にノードが設定されてしまってタコやイカが壁にめり込んでしまうため、シードはすべての壁から離れた任意の位置に置きます。
2. 画面の分割
次に指定したノードの間隔で画面を縦横分割します。画面の縦横の分割線の交点にシードがあるようにします。シードを基準として上下左右方向にノード間の距離を取っていくことで実現できます。
3. 画面をノードで埋め尽くす
2.でできた縦横の分割線の交点上にノードを作成します。
4. あるノードを起点として上下左右のノードをチェック
ノードを起点として上下左右のノードが有効かどうか判定します。ノード間に壁がある場合と、ノードが壁に近い場合(タコやイカが壁にめり込むため)はノードは無効になります。例えば図の3を使って設置したシードの上下左右のノードを見てみましょう。シードと上下左右のノードの間には壁はありません。シードの上下左右のノードは有効です。次にシードの一つ下のノードを起点に上下左右のノードを見てみましょう。こちらは上下と右のノードは問題ありませんが、左のノードは壁との距離が近すぎます。ゆえにノードとしては有効ではありません。
5. 有効なノードだけを残す
4.のロジックで有効なノードだけを残していきます。そのあとは残った有効なノードのさらに上下左右のノードを基準として同じことを繰り返して有効なノードを選別していきます。
6. エッジを作成する
4.と同じような図ですが考え方も同じです。基準とするノードとその周辺の8方向のノードを調べ、各々のノード間で壁がないかつ壁と近すぎなければエッジを作成します。間に壁があるまたは壁と近すぎる場合はエッジを作成しません。
7. すべてのノードでエッジを作成する
これは有効なノードをどの順番でもいいので片っ端から調べていきます。全て終われば完成です。
このようにして作成されたナビゲーショングラフは次の経路探索で使用します。
経路探索
経路探索は重み付けグラフのとあるノードからとあるノードに行く時に、最短コストとなる経由ノードを見つけることです。重みとは距離などのノード間を移動するときのコストのことです。
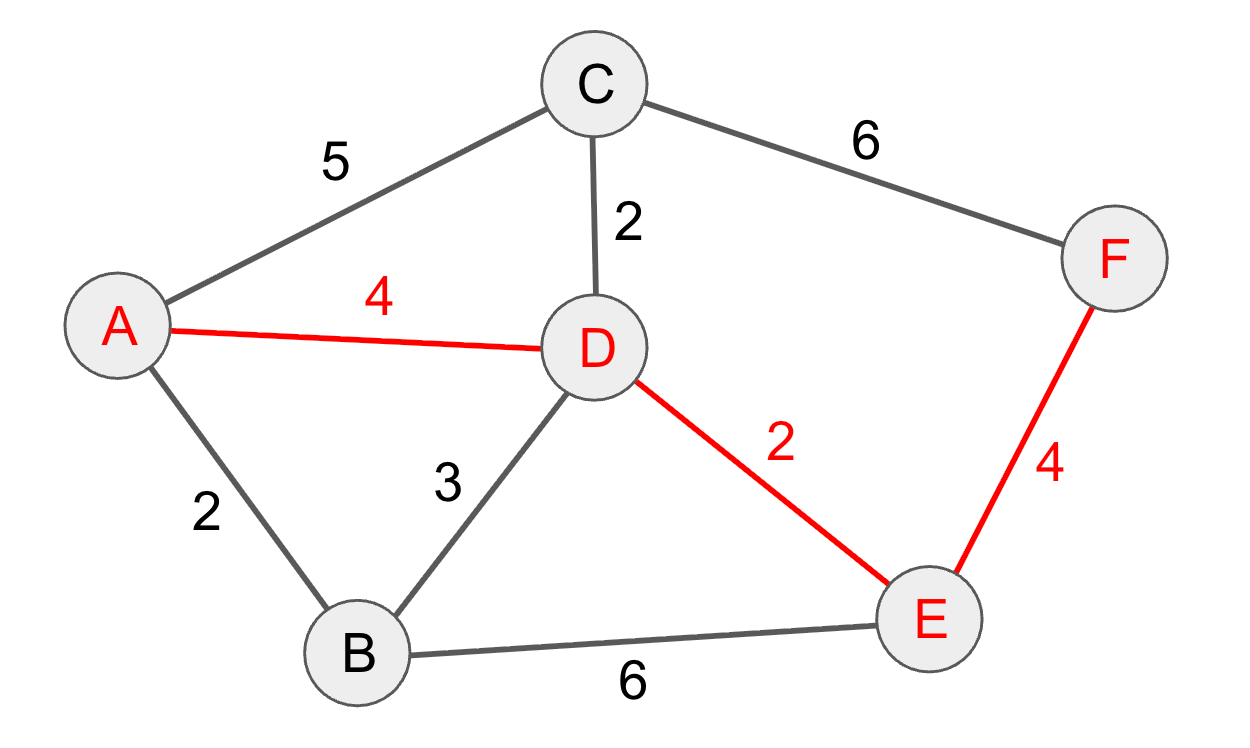
例えば上のグラフでAからFに移動するとき、A→D→E→Fと辿るのがコストが10で最短経路になります。この最短経路を探索するアルゴリズムが必要になります。なおイカタコ戦争ではノード間の距離がコストになっています。
経路探索で有名なのはダイクストラ法とその改良版であるA*アルゴリズム(エースターアルゴリズムと読む)ですが、ノード数をnとすると、両者とも計算量が
経路テーブルによる経路探索
下図の右側の表が経路テーブルです。この経路テーブルを用いてA→Fへの最短経路を求めます。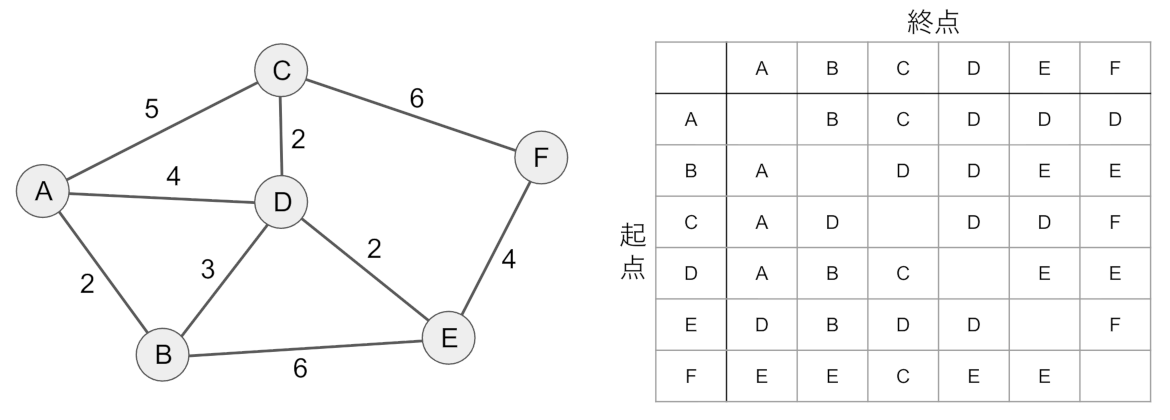
経路テーブルは起点から終点に最短で移動する時、起点から次に移動すべきノードを示しています。起点Aと終点Fの時、Dが次に移動すべきノードであることがわかります。
次にDからFに最短で移動すべきノードを探します。起点Dと終点Fの時、経路テーブルからEが次に移動すべきノードだとわかります。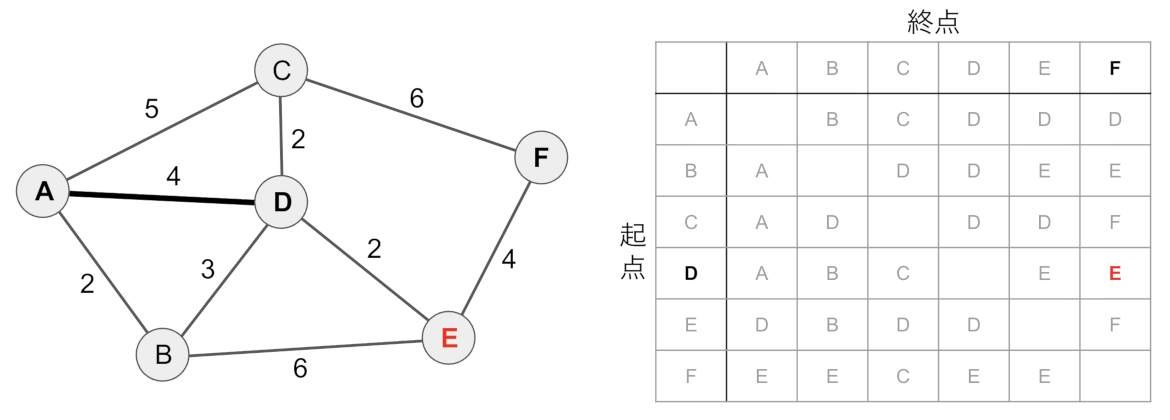
最後にEからFに最短で移動すべきノードを探します。経路テーブルから次に移動すべきノードがFであり、Fは終点でもあるので経路探索は終了です。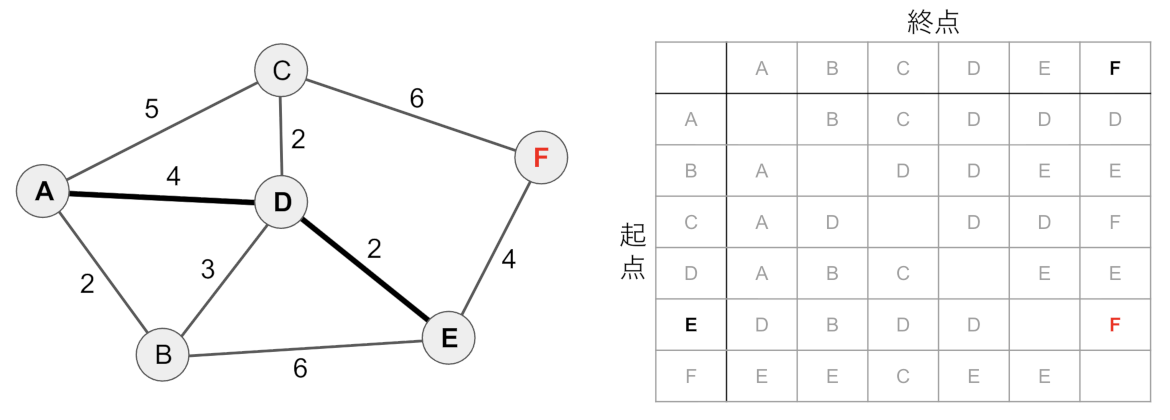
得られたノードを順番に並べると最短経路(A→D→E→F)が得られます。
マップで紹介したナビゲーショングラフに対してこの経路テーブルを作成します。この経路テーブルの作成には全点の対を求める必要があるのでワーシャル・フロイド法を用いました。生成AIに聞いたら割といい感じでコードを生成してくれました。
こうして作成した経路テーブルは先ほどのマップのデータの中に入っています。経路テーブルのデータは相当な大きさになるので、データ量を抑えるためにバイナリデータにしてzip圧縮しています。このマップデータを読み込んでオンメモリに経路テーブルを展開し、経路探索ではこの経路テーブルを使うことで高速な経路探索を実現しています。
ビヘイビアツリー
移動経路がわかると今度はノード間を順番に移動するロジックが必要になります。これは行動順を定義したツリー構造であるビヘイビアツリーを作って順番に処理をしています。
経路探索で使った経路のサンプルデータを使ってビヘイビアツリーを説明します。現在地のAからD、E経由でFに移動し、Fでアイテムを取得したのち、FからEを経由してBに移動する行動を考えます。右側にビヘイビアツリーを使って表しています
まずは「Dに移動」をすることを考えます。ゲームループで少しずつオブジェクトを動かし、Dに到達したと判定すれば次の「Eに移動」に行動を移します。
「Eに移動」が完了すると同じように「Fに移動」に移行し、「Fに移行」も終了すると今度は枝分かれの根元に戻り、「アイテム取得」を実行します。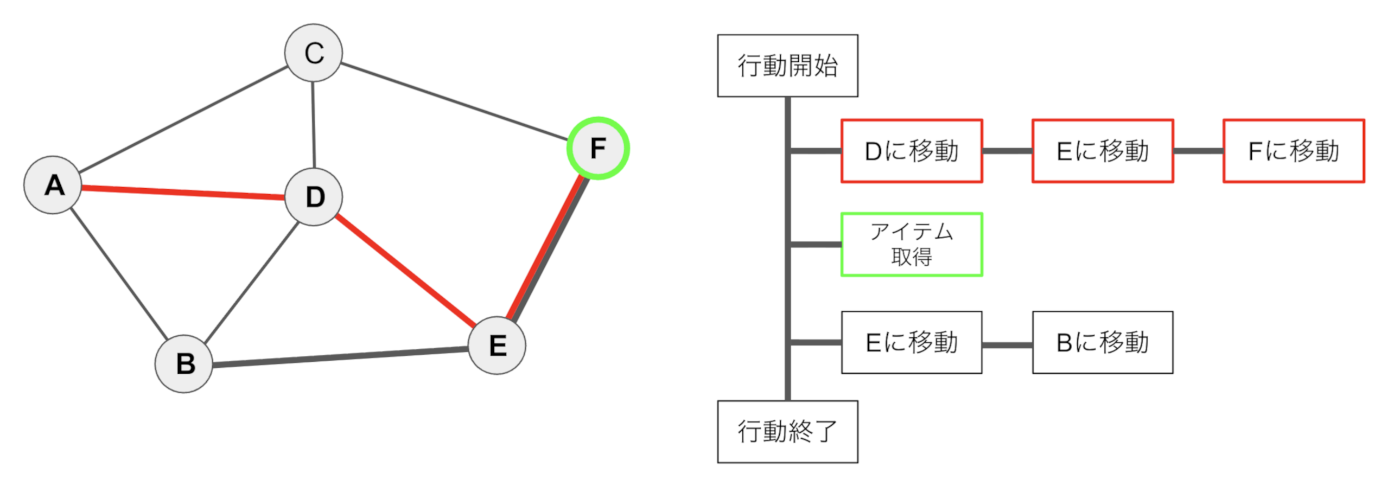
その後、「Eに移動」、「Bに移動」を実行して行動が終了します。最終的に図のオレンジの線のように上から行動が処理されていきます。これはツリーが深さ優先探索の順に処理されていることになります。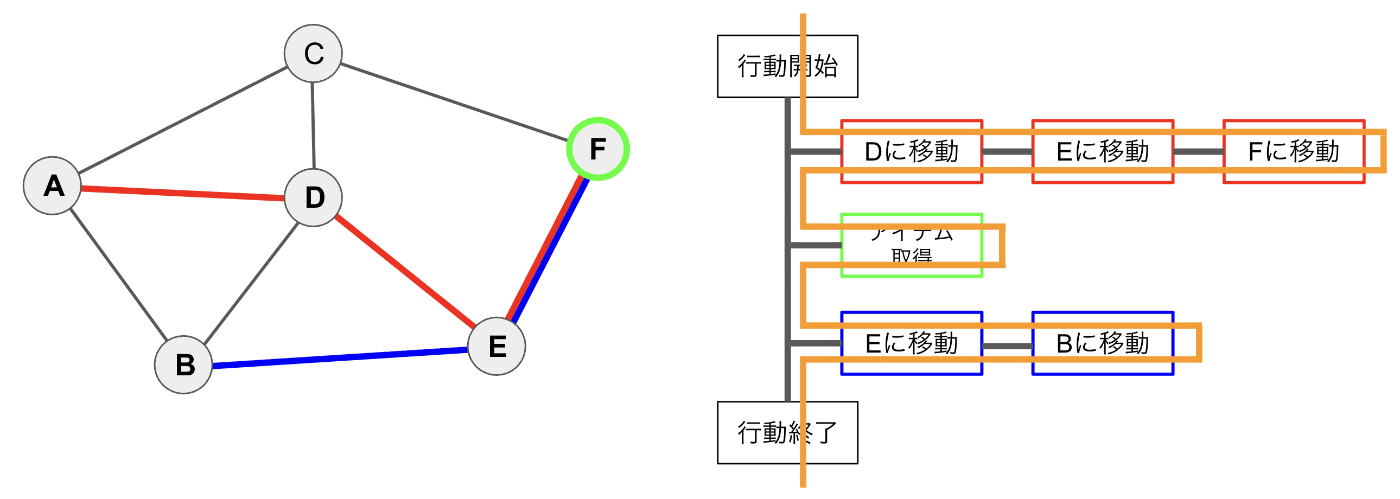
ビヘイビアツリーは並行して同時に複数の行動を行うことを定義することもできます。回転しながら移動する行動を考えます。A→Dは右回転、D→Eは左回転、E→Fは右回転しながら移動する行動を考えます。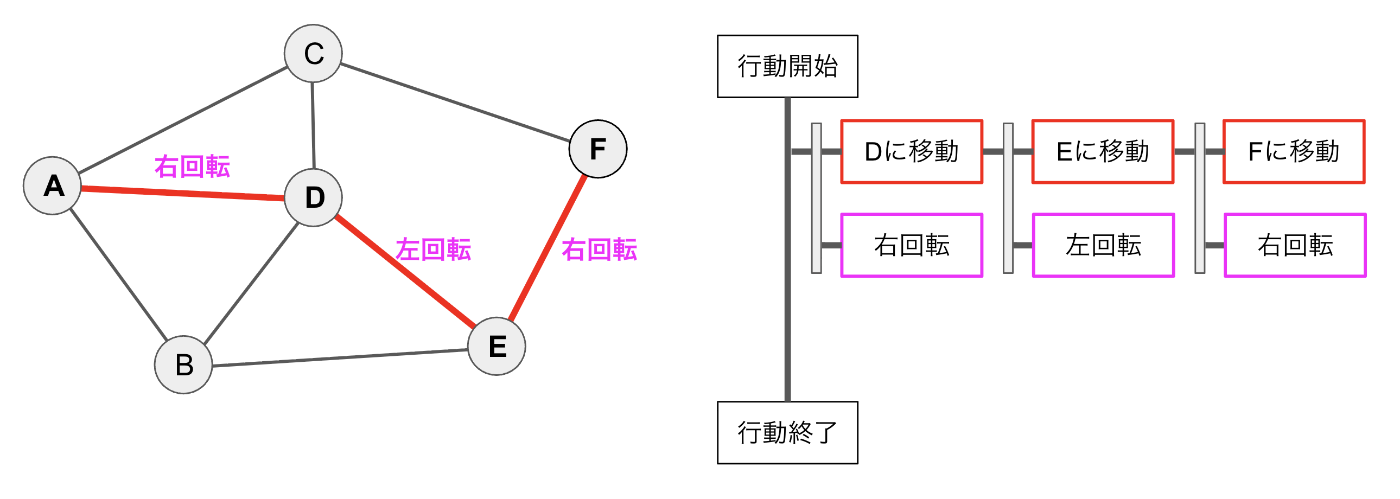
A→Dに右回転しながら移動する時、「Dに移動」というノードと「右回転」というノードを並列実行するコンテナに詰めて同時に処理をします。これはコンテナ内では幅優先探索をして見つかった行動をすべて同時に処理していることになります。ノードの処理が終わると次の処理に移行するのは今まで通りです。
ビヘイビアツリーの実装
ビヘイビアツリーはツリー構造のため、コンポジットパターンを使って実装できます。実装例を以下に示します。
interface Behavior {
finished: boolean;
update(): void;
}
class SingleNode implements Behavior {
finished: boolean = false;
constructor(private name: string) {
}
update() {
console.log(this.name)
this.finished = true;
}
}
class SequentialNodes implements Behavior {
finished: boolean = false;
constructor(private behaviors: Behavior[]) {
}
update() {
const behavior = this.behaviors[0];
behavior.update();
if (behavior.finished) this.behaviors.shift();
if (this.behaviors.length === 0) this.finished = true;
}
}
class ParallelNodes implements Behavior {
finished: boolean = false;
constructor(private behaviors: Behavior[]) {
}
update() {
this.behaviors.forEach((behavior, index) => {
behavior.update()
if (behavior.finished) this.behaviors.splice(index, 1);
})
if (this.behaviors.length === 0) this.finished = true;
}
}
単一処理のSingleNodeクラス、複数処理を順次実行で行うSequentialNodesクラス、複数処理を並列実行で行うParallelNodesクラスが定義されており、それぞれBehaviorインターフェースを満たしています。単一ノードと複数ノードがBehaviorインターフェースを満たすことで同じ振る舞いをするようになり、ツリー構造が実現できるようになります。
先ほど出てきた「Dに移動」→「Eに移動」→「Fに移動」→「アイテム取得」→「Eに移動」→「Bに移動」の行動を実装すると以下のようになります。
const behaviors1 = new SequentialNodes([
new SequentialNodes([
new SingleNode("Dに移動"),
new SingleNode("Eに移動"),
new SingleNode("Fに移動"),
]),
new SingleNode("アイテムを取得"),
new SequentialNodes([
new SingleNode("Eに移動"),
new SingleNode("Bに移動"),
])
]);
while (!behaviors1.finished) {
behaviors1.update();
}
こちらを実行すると実際にその通りに実行されます。
さらに先ほど出てきた「Dに移動+右回転」→「Eに移動+左回転」→「Fに移動+右回転」の行動も実装すると以下のようになります。
const behaviors2 = new SequentialNodes([
new ParallelNodes([
new SingleNode("Dに移動"),
new SingleNode("右回転"),
]),
new ParallelNodes([
new SingleNode("Eに移動"),
new SingleNode("左回転"),
]),
new ParallelNodes([
new SingleNode("Fに移動"),
new SingleNode("右回転"),
]),
])
while (!behaviors2.finished) {
behaviors2.update();
}
こちらも実行すると実際にその通りに実行されます。
ビヘイビアツリーを使うとゲーム内での複雑なロジックも簡潔に書けるようになります。ステートマシンを使ってコードがぐちゃぐちゃになってしまう場合は、ビヘイビアツリーの導入を検討してみましょう。
評価関数
ビヘイビアツリーで行動の制御ができるようになると、今度は行動を選択するためのロジックが必要になります。最適な行動を選択するときには評価関数を使います。その時点の状況下でとりうる行動の選択肢をスコア化し、スコアが最も大きい行動を選択します。このスコアを計算するのに用いるのが評価関数です。
例えばイカタコ戦争ではタコやイカが取りうる行動の選択肢の例として以下の3つが存在します。
- 回復アイテムを取りに行く
- 敵を攻撃する
- 指定の位置に移動
このうちのどれを選ぶかは、「残りライフの割合」、「回復アイテムまでの距離」、「敵までの距離」、「指定の位置に移動する指示が出ているか」など、その時点での状況で各々の行動の評価関数を使ってスコアを計算します。具体的にそれぞれの評価関数をどう設計するかみていきましょう。
1. 回復アイテムを取りに行く
回復アイテムを取りにいきたい時はどういう時かを考えます。残りライフが少ないほど回復アイテムを取りにいきたいけど、残りライフが多ければ特に回復アイテムを取りに行く必要はないでしょう。また回復アイテムが近くにあるほど取りにいきたいでしょう。この考えを元に評価関数を作ると以下のようになります。
| 変数 | 説明 |
|---|---|
| 残りライフ | |
| 回復アイテムまでの距離 | |
|
|
任意の係数 |
|
|
任意の定数 |
現時点の「残りライフ」が小さいほうがスコアが高くなるようにする、かつ「回復アイテムまでの距離」が小さいほうがスコアが高くなるように評価関数を設計します。任意の値の係数や定数はパラメータなのでゲームバランスをみながら微調整をしていきます。
2. 敵を攻撃する
次は敵を攻撃したい時はどういう時かを考えます。敵までの距離が近いほうが敵を攻撃したいでしょう。しかし、残りライフが少ない時は敵を攻撃したくありません。この考えを元に評価関数を作ると以下のようになります。
| 変数 | 説明 |
|---|---|
| 残りライフ | |
| 敵までの距離 | |
|
|
任意の係数 |
| 任意の定数 |
現時点の「敵までの距離」が小さいほうがスコアが高くなる、かつ「残りライフ」が高いほうがスコアが高くなるように評価関数を設計します。任意の値の係数や定数は先ほどと同じくパラメータなのでゲームバランスをみながら微調整をしていきます。
3. 指定の位置に移動
移動司令が出ている場合のみ指定の位置に移動します。この場合の評価関数は以下のようになります。
現時点の状態として「移動司令が出ている場合」は、「移動司令が出ていない場合」と比べて、指定位置に移動という行動をとりやすくするため、「移動司令が出ていない場合」より「移動司令が出ている場合」のほうがスコアが高くなるように評価関数を作成します。
3つの行動の評価関数ができました。この評価関数に更に調整用の係数(
かけて、現在の時点での行動のスコアを計算します。
| 行動 | スコア |
|---|---|
| 1. 回復アイテムを取りに行く | |
| 2. 敵を攻撃する | |
| 3. 指定の位置に移動 |
上の例では現時点の変数を使ってスコアを計算した結果、「1. 回復アイテムを取りに行く」のスコアが78となり、一番高くなりました。その時点での直前の行動と異なる場合は、それまでのビヘイビアツリーを破棄し、「1. 回復アイテムを取りに行く」のビヘイビアツリーを新たに作成して置き換えることで行動を切り替えます。
計算の途中で出てきた
センサーメモリ
敵を攻撃するには敵の位置を把握し続けることが必要です。しかし敵は動き続けるため、視界からいなくなってしまうこともあります。

このときに敵を追いかけず、攻撃をあきらめて別の行動をとってしまうとゲームとしての面白味がなくなってしまいます。イカタコ戦争では敵の位置を把握は主に視覚で行いますが、視覚によって敵の位置を把握した時点の敵の位置や速度などを記憶し、敵の将来位置を予測してその地点に向かわせています。
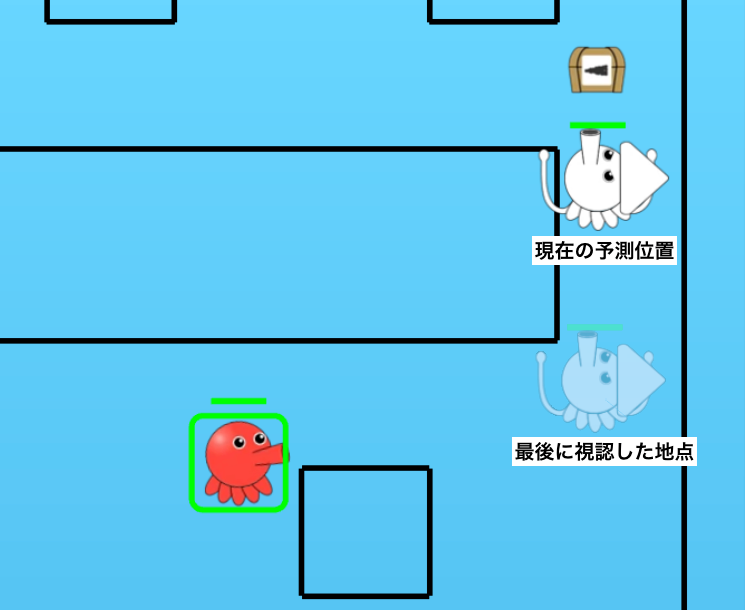
このように敵を把握するセンサーと、把握した時点のデータを保持するメモリ機能を合わせてセンサーメモリと呼びます。センサーとして視覚以外に聴覚も持つとか、メモリ機能としてどれくらいの期間ターゲットのデータを保持するかなどセンサーメモリの作り込みで動きがかなり変わってきます。工夫をして色々作り込んでみましょう。
空間分割
イカタコ戦争では非常に多くの当たり判定があります。例えばタコやイカが発射された弾にヒットしたか、発射された弾が壁に当たったかなどです。武器によっては弾を複数発射するものもあり、それらの当たり判定を全ての物体で計算すると、計算回数が膨大になってしまいます。例えば、ブラスターという武器は1回の攻撃で小さな弾を40個発射します。この40個がそれぞれ5体の敵との当たり判定を計算し、さらに44本の線分からなる壁との当たり判定を計算します。さらに、10体すべてのキャラクターがこの武器を同時に発射したとすると、その計算回数は
空間分割の考え方はシンプルです。まずは全体の空間をセルという小さい空間に分割します。そして物体がどの空間に位置するのかを計算し、自身が属するセルとその近辺のセルに属する物体のみとの当たり判定を計算します。こうすることで遠くにあるので計算が不要な物体との当たり判定の計算をスキップできます。

上図はイカタコ戦争での空間分割したセルの一覧です。ゲームの空間を均等に0~95番のセルで分割しています。

イカが発射したブラスターの弾の当たり判定を見ていきます。①の弾は65番のセルに属していますが、65番のセルに当たり判定の対象となるタコと壁はありません。ゆえに①の弾は当たり判定の計算回数は0回になります。一方②の弾は53番のセルに属しており、この53番のセルには2対のタコと3辺の壁(縦2本と横1本)が属しています。そのため計算量は
以上がイカタコ戦争のゲームロジックです。結構大変だなと思った方が多いんじゃないかなと思います。実際に実装しててもかなり大変でした。UnityやUnreal Engineといったゲームエンジンが普及している今は自前でこのような実装する必要性は全くないのですが、ゲームエンジンを使うと思うような挙動にならないとか、あえて軽量なゲームフレームワークで作りたい場合は自前で実装してみるのも選択肢になってくると思います。特に生成AIの登場で数学絡みの実装はかなり楽になってて、開発中もかなり助けられました。生成AIも積極的に使うことをお勧めします。また、イカタコ戦争は今回ご紹介したゲームロジック以外にも細かい工夫がたくさんあります。ご興味があれば「実例で学ぶゲームAIプログラミング」を参考にしてみてください。
Views: 0

