個人的な備忘録を兼ねたPyTorchの基本的な解説とまとめです。LSTMを利用した日経225を利用した予測の2回目となります。今回も次の日の日経225の始値を予測する単純な形ですが、前回(第8回)の1期ずれ予測(ナイーブ予測)からの改善とLSTMの理解の深化を目標としています。
方針
- できるだけ同じコード進行
- できるだけ簡潔(細かい内容は割愛)
- 特徴量などの部分,あえて数値で記入(どのように変わるかがわかりやすい)
演習用のファイル
再帰ネットワークは、$t$期のデータ$x_t$と$t-1$期までの過去の情報の特徴量である履歴$h_{t-1}$の2種類を使って、$t$期の特徴量を
$$h_t=\tanh(W_x x_t + W_h h_{t-1} + b)$$
のように導出していくタイプのネットワーク構造になります。
- $x_t$:$t$期での新しい入力データ
- $h_{t-1}$:前の期で計算した結果「過去の情報」
- $h_t$:現在計算している結果(これが次の時刻では過去の情報・履歴の$h_{t-1}$となる)
前回はRNNの中でもLSTMを利用して日経225の始値だけを利用して始値予測を行いました。結果は、きれいに1期ラグがある予測になりました。グラフを見ると様子がわかります。1期ずれた緑色の折れ線と予測値を表すオレンジ色の線が重なっているように見えます。
今回はこの「1期遅れている部分・ラグ」を少しでも改善してみたい!予測値を実測値に近づける試みを行います。結果から述べると次のようなグラフに改善されます。先程よりも実測値を表す青い線にオレンジ色の予測値がわずかながら近づいているのが確認できます。下図ではわかりにくいので、後半部分に期間を区切った拡大図も掲載しておきます![]()
数値的な判定は次回以降にします![]()
![]()
![]()
PyTorchによるプログラムの流れを確認します。基本的に下記の5つの流れとなります。Juypyter Labなどで実際に入力しながら進めるのがオススメ
- データの読み込みとtorchテンソルへの変換 (2.1)
- ネットワークモデルの定義と作成 (2.2)
- 誤差関数と誤差最小化の手法の選択 (2.3)
- 変数更新のループ (2.4)
- 検証 (2.5)
2.0 データについて
日経225のデータをyfinanceやpandas_datareaderなどで取得します。第8回と同一のデータを利用します。
| Date | Open | High | Low | Close | Volume |
|---|---|---|---|---|---|
| 2021-01-04 | 27575.57 | 27602.11 | 27042.32 | 27258.38 | 51500000 |
| 2021-01-05 | 27151.38 | 27279.78 | 27073.46 | 27158.63 | 55000000 |
| 2021-01-06 | 27102.85 | 27196.40 | 27002.18 | 27055.94 | 72700000 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 2025-06-18 | 38364.16 | 38885.15 | 38364.16 | 38885.15 | 110000000 |
| 2025-06-19 | 38858.52 | 38870.55 | 38488.34 | 38488.34 | 89300000 |
始値(Open)を予測する形で演習を進めていきます。始値のグラフを描画してみましょう。青色の線が日経225の始値の折れ線グラフとなります。
学習用データとテスト用データに分割します。グラフの赤い線の右側100期をテスト用のデータとして使います。残りの左側を学習用のデータとします。学習用データで学習させて、「右側の100期間を予測できるのか?」が主目標となります。
2021年以降の日経225の値は、3万円前後の数値になることがほとんどです。誤差計算時の損失の値が大きくなりすぎないように、変数の更新がうまく行われるように、「1万円で割り算して数値を小さく」 しておきます。これで、ほとんどの値が2.5〜4に収まるはずです。正規化と呼ばれる格好良い手法を使うと更に精度も向上していきます。
2.1 データの読み込みとtorchテンソルへの変換
CSVファイルをpandasで読み込み、RNNで学習できる形にデータを前処理します。具体的には、株価の始値・高値・安値・終値データを窓サイズ5で区切って、その窓を1つずつスライドさせながらデータセットを作成していきます。前処理の具体的な解説は第8回を参照してください。
CSVファイルの読み込みから窓サイズでの分割までのコードです。スマートに一度に変換ではなく、地味に4種類同じことを繰り返す形で書きました![]()
データの読み込みと前処理
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
# CSVファイルの読み込み
data = pd.read_csv("./data/nikkei_225.csv")
# 日経225の値を10,000円で割り算して値を小さくする
scaling_factor = 10_000
x_open = data["Open"]/scaling_factor
x_high = data["High"]/scaling_factor
x_low = data["Low"]/scaling_factor
x_close = data["Close"]/scaling_factor
# 窓サイズ5で区切る
win_size = 5
XO = [x_open[start:start+win_size] for start in range(len(data)-win_size)]
XH = [x_high[start:start+win_size] for start in range(len(data)-win_size)]
XL = [x_low[start:start+win_size] for start in range(len(data)-win_size)]
XC = [x_close[start:start+win_size] for start in range(len(data)-win_size)]
T = x_open[win_size:]
窓サイズ5で区切った4種類のデータを(XO、XH、XL、XC)、教師データのリストをTとします。今回のポイントは、窓サイズ5で区切った始値・高値・安値・終値の4種類を入力データに使う点です。 非常にシンプルですが、これだけでも改善が見られます ![]()
5個区切りデータ(XO、XH、XL、XC)を結合して、(バッチサイズ、5,4)の形状に変換して入力用のデータにします。
実際に表示するとわかるのですが、上記のコードだとXOやTはタイプが入り乱れています。最終的にtorch.FloatTensor()の形になればよいので、スマートではありませんが力技で押し切るコードにしました ![]() 一旦、numpy配列にして形式を整えてしまいましょう
一旦、numpy配列にして形式を整えてしまいましょう![]()
![]()
![]()
データの結合
# numpy配列に変換!形式を整えるぞ
xo = np.array(XO)
xh = np.array(XH)
xl = np.array(XL)
xc = np.array(XC)
t = np.array(T)
xo = xo.reshape(xo.shape[0], xo.shape[1], 1)
xh = xh.reshape(xh.shape[0], xh.shape[1], 1)
xl = xl.reshape(xl.shape[0], xl.shape[1], 1)
xc = xc.reshape(xc.shape[0], xc.shape[1], 1)
# xo, xh, xl, xcの形状1の部分(axis=2)でデータを並べる
x = np.concatenate([xo, xh, xl, xc], axis=2)
# x.shape => (1087, 5, 4)
# t.shape => (1087,)
利用するデータの形状が、(バッチサイズ、系列長の5、特徴量の4)になっていることが確認できます。xをLSTMに入れることからネットワークが始まります。その前に、xとtをFloatTensorに変換して、学習用データとテスト用データに分割します。
torchテンソルへ変換
# 今回からGPU使えるときはGPUを利用、それ以外だとCPUになるような設定にします
device = "cuda" if torch.cuda.is_available() else "cpu"
x = torch.FloatTensor(x).to(device)
t = torch.FloatTensor(t).to(device).shape(-1,1) # 回帰問題なので(バッチサイズ, 1)
前半部分を学習用、後半部分をテスト用と前後に分割します。あとで数値的な検証や仮説検定をする予定なので100期ほどテストデータとして確保しておきます。
学習用とテスト用に分割
period = 100
x_train = x[:-period]
x_test = x[-period:]
t_train = t[:-period]
t_test = t[-period:]
# 入力する特徴量は1次元
# x_train.shape : torch.size([987, 5, 4])
# x_test.shape : torch.Size([100, 5, 4])
# t_train.shape : torch.Size([987, 1])
# t_test.shape : torch.Size([100, 1])
2.2 ネットワークモデルの定義と作成
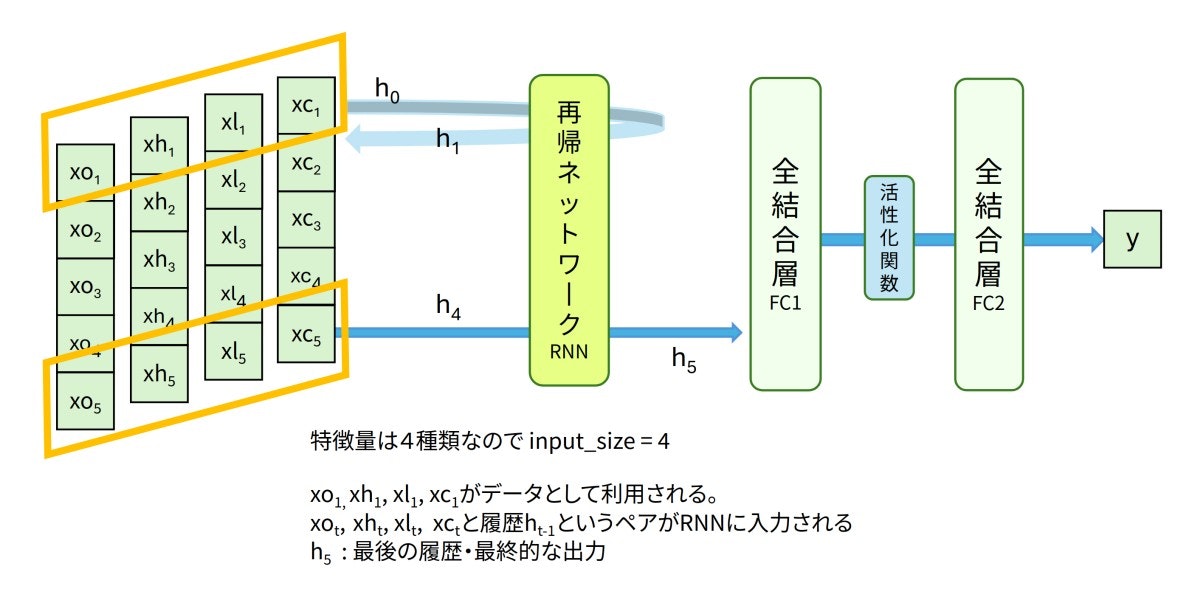
今回は下図のようなLSTMと全結合層を利用したネットワークで時系列予測を扱っていきます。入力データは窓サイズ5の日経225データです。オレンジ色っぽい平行四辺形で囲われた4次元の値$(xo_1, xh_1, xl_1, xc_1)$から順番にLSTMへ入力されます。LSTMに入力される特徴量は4つなので、input_size=4となります。最終的な出力であるh5が過去の5日分の情報を再帰的に考慮した特徴量となります。特徴量h5から全結合層を経由して最終的に翌日の予測値 y が計算されます。
PyTorchでのLSTMの書き方のポイントをまとめておきます。
LSTM層の書き方
nn.LSTM(input_size, hidden_size, num_layers, batch_first)
- input_size : 入力される特徴量の次元
- hidden_size : 出力される隠れ層の特徴量の次元
- num_layers : 再帰するLSTMの数、デフォルトはnum_layers=1
- batch_first : Trueで(バッチサイズ、系列長、特徴量)の形状
batch_first=TrueでのLSTMの出力値
o, (h, c) = lstm(x)
- o : すべての時点での最終層(一番最後layer)の隠れ状態の出力
- h : 最後の時点でのすべての隠れ層の出力
- c : 最後の時点におけるセル状態
詳細はPyTorchの公式ドキュメントに記載されています。
oとhの違いは第8回を参考にしてください。
上図「LSTM→全結合層→全結合層」のネットワーク構造をコード化していきます。利用している数値ですが、input_size=4を除いてすべて第8回と等しい値になっています![]()
モデル定義
class DNN(nn.Module):
def __init__(self):
super().__init__()
self.rnn = nn.LSTM(input_size=4 ,hidden_size=100, num_layers=1, batch_first=True)
self.fc1 = nn.Linear(100, 50)
self.act1 = nn.ReLU()
self.fc2 = nn.Linear(50, 1)
def forward(self, x):
o, (h, c) = self.rnn(x)
last_output = h[-1] # 最後のステップの出力 o[:,-1,:]でも同じ
h = self.fc1(last_output)
h = self.act1(h)
y = self.fc2(h)
return y
model = DNN()
model.to(device)
LSTMの最後の出力であるh[-1]かo[:,-1,:]を全結合層への入力とします。print(model)の結果はとてもシンプルです。
modelの構造
DNN(
(rnn): LSTM(4, 100, batch_first=True)
(fc1): Linear(in_features=100, out_features=50, bias=True)
(act1): ReLU()
(fc2): Linear(in_features=50, out_features=1, bias=True)
)
2.3 誤差関数と誤差最小化の手法の選択
回帰問題なので予測値y と実測値(教師データ)t の二乗誤差を小さくしていく方法で学習をすすめます。
# 損失関数と最適化関数の定義
criterion = nn.MSELoss() # 平均二乗誤差
optimizer = torch.optim.AdamW(model.parameters())
2.4 変数更新のループ
LOOPで指定した回数
- y=model(x) で予測値を求め、
- criterion(y, t_train) で指定した誤差関数を使い予測値と教師データの誤差を計算、
- 誤差が小さくなるようにoptimizerに従い全結合層の重みとバイアスをアップデート
を繰り返します。
学習ループ
LOOP = 8_000
model.train()
for epoch in range(LOOP):
optimizer.zero_grad()
y = model(x_train)
loss = mse(y,t_train)
if (epoch+1)%500 == 0:
print(epoch,"\tloss:", loss.item())
loss.backward()
optimizer.step()
forループで変数を更新することになります。損失の減少を観察しながら、学習回数や学習率を適宜変更することになります。ここまでで、基本的な学習は終わりとなります。回数などは損失の減少を見ながら適当![]() 〜に判断しましょう。
〜に判断しましょう。
2.5 📈 検証
テストデータ x_test と t_test を利用して学習結果のテストとなります。x_testをmodelに入れた値 y_test = model(x_test) が予測値となります。グラフを利用して視覚的に検証!1期ずれた状態からやや改善しているかな![]()
![]()
![]()
予測値と実測値のグラフ
import matplotlib.pyplot as plt
import japanize_matplotlib
model.eval()
y_test = model(x_test)
prediction = y_test.detach().cpu().numpy()
real = t_test.detach().cpu().numpy()
# 一つ前の期の実測値も示したい
e = period
plt.figure(figsize=(15,8))
plt.plot(real[1:e], label="real", marker="^")
plt.plot(prediction[1:e], label="prediction", linestyle="dotted", marker="*")
plt.plot(real[:e-1], label="1期ずれ", marker="+")
plt.legend()
plt.title(f"テストデータでの検証「最後の{period}期」")
plt.show()
1期ずれたナイーブ予測も比較表示したいので、実測値と予測値の開始の時点が1になっています。
- 実測値:
plt.plot(real[1:e]) - 予測値:
plt.plot(prediction[1:e]) - 1期ずれ:
plt.plot(real[:e-1])
100期間だとグラフの差がわかりにくいのでテスト用データの1期から50期でグラフ判定!実測値の青い線とナイーブの緑線の間に予測値のオレンジ色の線が見えると思います。大雑把ではありますが、1期ずれのナイーブ予測から改善しているのではないでしょうか?パラメータをいじることでもう少し実測値に寄り添いますが割愛 ![]()
![]()
![]()
![]()
![]()
ナイーブ予測の緑線より作成したモデルの予測が大きく外れている箇所もいくつか見られますが、概ね、ナイーブ予測よりも良い結果に見えるかな。たまたまなのですが、検証の冒頭50期間は右下がり状態ですね📉
- グラフによる見た目判定ではなく、数値で比較してみたいと思います

- 今回のモデルはナイーブ予測よりも有意なの?を検証していく予定です
Views: 1