民主主義は数学的に不可能なのか？ – GIGAZINE

科学や教育に関するさまざまな話題を動画で解説するYouTubeチャンネル・Veritasiumが、「なぜ民主主義は数学的に不可能なのか」と題し、選挙における投票システムについて動画で解説しています。

Why Democracy Is Mathematically Impossible – YouTube

民主主義における最も単純な選挙方法として、有権者に投票用紙で一人の候補者を選ばせる方式があります。この方式は「単純小選挙区制」として知られており、単に最多得票の候補者が勝利します。この方法は古代にまでさかのぼり、14世紀からイギリスの下院議員選出に使用され、現在も世界44カ国で指導者選出に用いられています。

しかし、単純小選挙区制には問題があります。議会の代表者を選ぶ場合、国の大多数が権力を握る政党に投票していないという状況が頻繁に発生します。過去100年間で、イギリス議会で単一政党が議席の過半数を占めた事例は21回ありましたが、その政党に実際に過半数の有権者が投票したのはわずか2回だけでした。つまり、少数派の支持しかない政党が権力を握ることになります。

また、単純小選挙区制では「類似した候補者が互いから票を奪い合う」という現象も起こります。2000年のアメリカ大統領選挙は、本質的には民主党のアル・ゴアと共和党のジョージ・W・ブッシュの間の選挙でした。当時、全米の全州が単純小選挙区制を採用していました。

ブッシュはフロリダ州で非常に僅差で勝利しましたが、もう一人の候補者にラルフ・ネーダーがいました。ネーダーは緑の党の候補者で、ゴアやブッシュよりも明らかに左派でした。ネーダーは「市民の懸念、人々の懸念、貧しい人、富裕層、中流階級の高まりが、特別利益の権力に対抗するために必要だ」と主張し、フロリダ州でほぼ10万票を獲得しました。「ブッシュかゴアに良心的に投票できるかわからない。ラルフ・ネーダーに投票する」と述べる有権者もいました。

しかし、ネーダーに投票した大多数の有権者は、ゴアではなくブッシュが当選したことに愕然としました。これは「スポイラー効果」と呼ばれます。ほとんどのネーダー支持者はブッシュよりゴアを好んでいましたが、この投票方式では一人の候補者にしか投票できないため、その傾向を表現する方法がありませんでした。したがって、単純小選挙区制は有権者に戦略的な投票が求められます

単純小選挙区制は勝者総取り制の投票システムであり、より大きな政党への権力集中につながり、最終的には二大政党制を導くことになります。このように、選挙において候補者数が収束していく現象は「デュヴェルジェの法則」と名付けられています。

単純小選挙区制には問題があるとすれば、他にどのような方法があるでしょうか。候補者が選挙に勝つためには過半数、すなわち50％プラス1票以上を獲得しなければならないと定めるのは1つの解決法で、選挙で誰も過半数を得られなかった場合は、最も少ない票を得た候補者に投票した人々に別の候補者に投票するよう求め、一人の候補者が過半数に達するまでこのプロセスを繰り返します。しかし、何度も選挙を行うのは大変な手間です。

そこで、有権者に好きな順に候補者の順位をつけてもらい、好きな候補者が落選した場合は次の選択肢に移行するという「優先順位付投票制」があります。投票が締め切られると、有権者の第一選択を集計します。過半数の票を得た候補者がいれば、その候補者が勝者となります。しかし過半数を得た候補者がいない場合は、最も少ない票を得た候補者が除外され、その票は有権者の第二選択肢に配分されます。これを一人の候補者が過半数を得るまで続けます。数学的には繰り返し選挙を行うのと同じですが、時間と手間を省くことが可能です。

優先順位付投票制は有権者だけでなく、候補者の互いへの振る舞いにも影響します。2013年のミネアポリス市長選挙では、このランク選択投票が使用されました。当時現職市長が退任した時に多くの人々が市長になりたいと立候補し、35人の候補者がそろいました。

35人の候補者がいれば、互いを攻撃したり注目を集めようとしたりするだろうと思われますが、実際にはそうならず、35人の候補者全員が互いに非常に親切で丁寧に接しており、最終市長討論会の終わりには、全員が集まって歌を一緒に歌うほどだったそうです。

しかし、優先順位付投票制にも問題があります。候補者が悪い結果を出すことで、実際に当選につながる場合があります。例えば、アインシュタイン、キュリー、ボーアという3人の候補者がいるとします。アインシュタインとボーアは非常に対立する見解を持ち、キュリーはイデオロギー的に中間にいます。

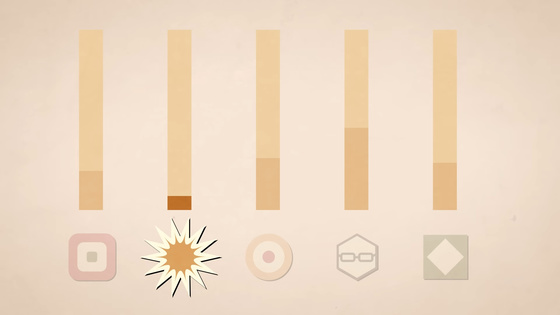
そして、投票の結果、アインシュタインが25％、キュリーが30％、ボーアが45％の票を得たとします。誰も過半数を獲得していないので、第二ラウンドに進み、アインシュタインが脱落します。アインシュタインに投票した人々が第二選択としてキュリーを選んだため、最終的にキュリーが当選します。

ところが、ボーアが酷い選挙演説をしたり、非常に不人気な政策を提案したりして、彼の支持者の一部がアインシュタイン側に移ったとします。すると今度はキュリーが脱落することになります。彼女は穏健派なので、彼女の支持者の半分がアインシュタイン、もう半分がボーアを第二ラウンドで選びます。これによりボーアが勝利します。つまり、ボーアが第一ラウンドで悪い結果を出したことが、実際に彼の当選につながるということです。これは投票システムとして望ましくありません。

これはフランスの数学者ニコラ・ド・コンドルセも考えていたことです。コンドルセは、論理と数学を厳密に投票システムの研究に適用した最初の人物の一人であり、社会選択理論と呼ばれる数学の一分野の創始者の一人です。彼はフランス革命の時代に活動していたため、人々の意思を公平に決定することはその当時の文化的な関心事でした。

1784年、フランス王立科学協会のジャン=シャルル・ド・ボルダがある投票方法を提案しました。有権者に候補者の順位をつけてもらいます。5人の候補者がいる場合、誰かを1位にすると、その候補者に4ポイントが与えられます。2位なら3ポイント、というように、最下位は0ポイントとなります。しかし、ボルダ方式には、「各候補者に与えられるポイントの数は、候補者の総数に依存する」という問題がありました。勝つ見込みのない余分な人を加えることは、勝者に影響を与えかねません。

そこで1785年、コンドルセは新しい投票システムを提案したエッセイを発表しました。この投票システムは「コンドルセ方式」と呼ばれています。

コンドルセ方式では、勝者は一体一の選挙で他のすべての候補者に勝つ必要があります。しかし実際には、多数の候補者がいる場合に多くの一対一の選挙を別々に行う必要はありません。その代わりに、有権者に候補者の好みの順位をつけてもらい、各候補者が他の各候補者よりも高く評価された投票数を集計します。

たとえば3人が食事をする時に、ハンバーガー・ピザ・寿司の3つの選択肢があるとします。1人目はハンバーガー＞ピザ＞寿司、2人目はピザ＞寿司＞ハンバーガー、3人目は寿司＞ハンバーガー＞ピザで好みの順序を決めていたとします。

ここでハンバーガーを選ばれた場合、2人目と3人目は「寿司が代わりに選ばれるべきだった」と主張できます。3人のうち1人だけが1人だけがハンバーガー＞寿司で、あとの2人は寿司＞ハンバーガーという序列だからです。しかし、同じ議論で、ピザは寿司より好まれ、バーガーはピザより好まれることになります。こうなると議論が堂々巡りになってしまいます。

この状況は「コンドルセのパラドックス」として知られています。しかし、コンドルセ本人はこの問題を解決する前に、フランス新政府の新憲法を批判したことで投獄され、獄中死しました。

その後150年間、多くの数学者が独自の投票システムや、コンドルセやボルダのアイデアの修正を提案しました。童話「不思議の国のアリス」の著者であるルイス・キャロルも、本名のチャールズ・ドジソン名義でこの問題に取り組んでいましたが、解決することはできませんでした。

1951年、アメリカの経済学者であるケネス・アローは「社会的選択と個人的価値」と題した論文を発表し、その中で、公正な選挙制度では以下の5条件を満たすことが必要だと主張しました。

条件1： 全会一致
もしグループの全員がある選択肢を別の選択肢より好むなら、グループ全体としてもその選択肢を好むべきです。例えば、もし全員が寿司をピザより好むなら、集団的な意思決定としても寿司をピザより好むべきだということです。

条件2：非独裁制
一人の好みだけが全体の決定を左右すべきではありません。つまり、もし全員がピザに投票し、一人だけが寿司に投票した場合、グループはピザを選ぶべきです。決定権が一人だけにあるなら、それは民主主義ではなく独裁制です。

条件3：定義域の非限定性
投票システムはどのような投票パターンでも処理できなければなりません。有権者は自由に好きな順位をつけることができ、投票システムは問題のある投票をスキップしたり、ランダムに結果を出したりせず、同じ投票セットに対して常に同じ結果を出さなければなりません。

条件4：推移性
集団的選好は論理的に整合性があるべきです。もしグループがバーガーをピザより好み、ピザを寿司より好むなら、バーガーを寿司より好むべきです。これは矛盾のない順序づけを保証します。

条件5：無関係な選択肢からの独立性
二つの選択肢間の集団的選好は、他の選択肢の存在や不在によって変わるべきではありません。例えば、寿司とピザの間の選好順位は、バーガーという第三の選択肢が導入されても変わるべきではありません。

しかし、アローはこれら5つの条件すべてを満たす投票システムは存在しないことを証明しました。これがアローの不可能性定理であり、この功績が認められ、アローは1972年にノーベル経済学賞を受賞しています。

では、民主主義は数学的に不可能な仕組みなのでしょうか。「選択する候補者が3人以上いる場合、有権者の選好を合理的に集約するための方法は存在しない」と論じるアローの不可能性定理はそう言っているように見えます。しかし、1948年、数学者のダンカン・ブラックは「委員会決定と選好の合理性」という論文を発表し、その中で中位投票者定理を発表しました。この中位投票者定理は、アローの不可能性定理よりも楽観的な見方を提供します。

ブラックが提唱した中位投票者定理は、有権者の選好が左派から右派といった単一の政治的次元に沿って分布し、各有権者の選好が特定の位置から離れるほど選好が下がる「単峰型」である場合、政治的スペクトラムの真ん中に位置する「中位投票者」の選好が多数決投票において勝利するというものです。

中位投票者定理は、なぜ多くの民主主義国家の政党が中央に収束する傾向があるのかを説明し、アローの不可能性定理が示した厳しい制約が特定の条件下では回避可能であることを示しながら、民主主義的意思決定システムが完全に機能不全ではなく、現実世界において合理的な結果をもたらしうることを示唆しました。

アローの不可能性定理は、有権者が候補者を他より上位にランク付けする「序数的投票システム」にのみ適用されます。しかし、有権者が候補者に対してランク付けではなく支持する度合を表明する「評価投票システム」は、アローの不可能性定理の制約を受けません。

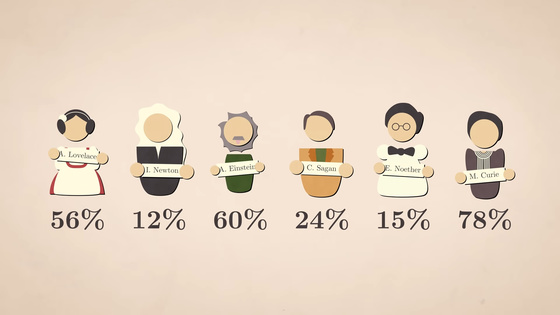
評価投票システムで最もシンプルな手法が「承認投票」で、有権者は支持する候補者全員にチェックを入れ、、最も多くの承認を得た候補者が勝利します。研究によれば、承認投票は投票率を上げ、ネガティブキャンペーンを減らし、第三の候補者や小政党の候補者がイデオロギー的に近い主要候補の当選を妨げるスポイラー効果を防ぐことがわかっています。

有権者は投票する党の規模を心配することなく、候補者への承認を表明できます。また、集計も簡単で、各候補者を承認する投票者の割合を数え、最も承認率が高い候補者が勝ちます。アローは最初、評価投票システムに懐疑的でしたが、晩年は評価投票システムが恐らく最良の方法であることを認めています。

実はこの承認投票は、1294年から1621年までバチカンの司祭がローマ教皇を選出するのに使用されています。また、国連事務総長の選出にも使用されていますが、大規模な選挙では広く使用されていません。

ウィンストン・チャーチルは「民主主義はこれまで試みられた他のすべての形態を除けば最悪の政府形態だ」という言葉を残しています。Veritasiumは「確かに民主主義は完璧ではありませんが、私たちが持っている最善のものです」とコメントしました。