100年以上解けなかった物理学の難問が、ついに数学の力で解けました。
アメリカのミシガン大学(U-M)で行われた研究によって、原子一粒の衝突から台風規模の渦までを貫く“一本の数学的な鎖”を初めて構築し、流体力学における3つの主要理論を統合することに成功したのです。
これまでの物理学では個々の粒子レベル、粒子の集団レベル、巨大な流体レベルを異なる数式で記述しており、まるで別々の法則のように扱われていました。
しかし今回の成果により3つの理論を連結させ、1900年から数学者たちを悩ませてきた「ヒルベルトの第六問題」の重要な部分を解決する大仕事となりました。
三つの理論を連結する“数学的鎖”は、どのように鍛え上げられたのでしょうか?
研究内容の詳細は2025年03月3日に『arXiv』にて発表されました。
目次
- “ビリヤード球”と“連続体”を同じ教科書に載せる挑戦
- ヒルベルト第六問題ついに崩れる:粒子から台風まで“一本の数学的鎖”で貫通
- 理論の土台が固まると、空も海も計算しやすくなる
“ビリヤード球”と“連続体”を同じ教科書に載せる挑戦

日常で目にする流体の動き(水の流れ、空気の渦など)は、実は無数の微小な粒子(分子)の集団運動です。
しかし、この現象を理解する方法には3つの視点(理論)が存在します。
1つ目はミクロ(微視的)な理論: 流体を構成する一粒一粒の分子に着目する視点です。
分子はまるで小さなビリヤード球のように動き回り、衝突します。
このレベルではニュートンの運動法則(古典力学)が適用され、各粒子の位置と速度を追跡することで振る舞いを説明できます。
しかし粒子の数は天文学的に多いため、全てを逐一計算するのは現実的ではありません。
2つ目は中間(メソスコピック)な理論: 巨大な粒子集団全体の振る舞いを統計的に捉える視点です。
19世紀の物理学者ルートヴィッヒ・ボルツマンは、このアプローチとしてボルツマン方程式を考案しました。
個々の分子ではなく「典型的な粒子」の振る舞い確率に注目し、粒子集団の平均的な性質(圧力や温度など)の時間変化を記述します。
ボルツマン方程式により、いちいち粒子一つひとつを追わなくても、気体や流体のだいたいの挙動を計算できるようになりました。
3つ目はマクロ(巨視的)な理論: 流体を連続的な物質とみなし、連続体の力学として扱う視点です。
個々の粒子の存在は無視し、流体を滑らかな一つの媒体ととらえて、その速度や圧力、密度場の変化を記述します。
これを可能にするのがオイラー方程式やナビエ-ストークス方程式(および関連する方程式群)です。
オイラー方程式は粘性(流体のねばり)を持たない理想流体の運動を表す基本方程式です。
ナビエ-ストークス方程式は粘性のある流体の運動を表す基本方程式で、エンジニアは航空機の設計や気象予測に日常的に活用しています。
以上の3つの理論はいずれも同じ現実の現象(流体の流れ)を違うスケールで説明したものです。
理想を言えば、ミクロの理論から一段階ずつ論理を積み上げていけば中間理論が導かれ、さらにそれを土台にマクロな理論が導かれるはずです。
ところが実際には、この「ミクロ→中間→マクロ」をつなぐ論理の橋渡しは非常に難しく、19世紀以来ずっと明確に示されてきませんでした。
古典物理はしばしば完成されていると考えられがちですが、未だに各法則間は意外に統一されていないのです。
そこでドイツの数学者ダフィット・ヒルベルトは、1900年に開催された国際数学者会議で「物理学を数学の公理体系で再構築する」という大胆な課題を提示しました。
これが有名なヒルベルトの第六問題です。
ヒルベルトはとくに例として気体分子の力学(ボルツマンの理論)を挙げ、ニュートンの運動法則のような「ミクロの基本法則(公理)」からオイラー方程式・ナビエ-ストークス方程式のような「マクロの法則(定理)」を導けるか問いかけました。
簡単に言えば、「気体分子のゴツゴツした衝突から出発して、統計的な方程式を経由し、連続体の方程式に至るまで、一貫した数学的論理で物理法則を組み立てよ」という挑戦です。
しかしこの挑戦は極めて困難で、部分的な成果はあっても誰も完全には成し遂げられずにいました。
こうした中、アメリカのシカゴ大学の数学者Yu Deng(鄧宇)氏と、ミシガン大学のZaher Hani氏、Ma Xiao(馬霄)氏からなる研究チームがこの難題に挑みました。
彼らの研究目的は、ニュートンの運動法則 → ボルツマン方程式 → オイラー/ナビエ-ストークス方程式という3段階の論理的つながりを厳密に構成し、ヒルベルト第六問題への回答を示すことでした。
ヒルベルト第六問題ついに崩れる:粒子から台風まで“一本の数学的鎖”で貫通

研究チームは、このミクロからマクロへの橋渡しを二段階のアプローチで実現しました。
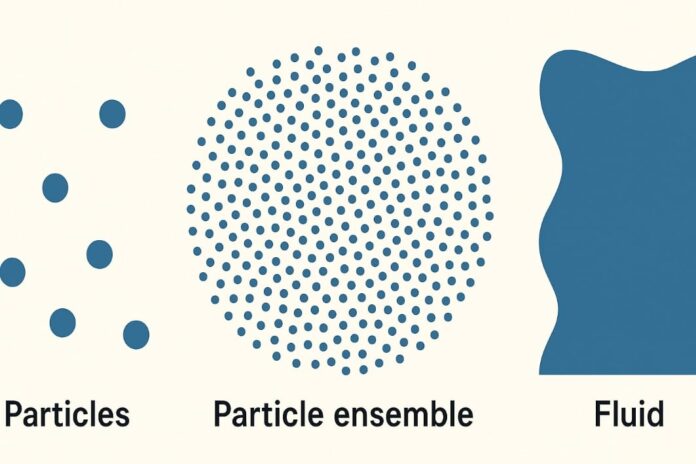
ニュートンの粒子力学(左)からボルツマンの運動論的方程式(中間)を経て、流体力学の方程式(右)へと至る論理の連鎖。
今回の研究では、この図に示されたミクロ→中間→マクロのすべての段階を一貫して証明した。
ミクロから中間(ニュートン力学 → ボルツマン方程式)
まず研究チームは、無数の粒子が飛び交い衝突するミクロな系から、ボルツマン方程式という統計的な記述が現れることを証明しました。
彼らが扱ったのは、直径が極めて小さい硬い球(ビリヤード玉のような粒子)同士が弾性的に衝突する理想化された気体模型です。
粒子数を非常に大きく、粒径を非常に小さくとる極限(ボルツマン・グラッド極限と呼ばれます)では、粒子の衝突頻度が一定に保たれつつ、粒子系全体の確率的振る舞いがボルツマン方程式の解に収束することを示しました。
直感的に言えば、「粒子が無数に存在すると仮定すれば、典型的な粒子の振る舞いはボルツマン方程式で記述できる」ことを数学的に裏付けたのです。
このステップ自体は古くから物理学者が考えてきたもので、1970年代にオスカー・ランフォードによってごく短い時間については証明されていました。
しかし長時間にわたって成り立つことを厳密に示すのは困難で、衝突を繰り返すうちに粒子の運動がどれだけ複雑になってもボルツマン方程式が成り立ち続けるのか、誰も証明できずにいたのです。
今回Deng氏らのチームは、新しい数学的手法を駆使して粒子衝突の履歴を厳密に追跡し、その累積効果が無視できるほど小さいことを示すことで、この長年の難関を突破しました。
難しく聞こえるかもしれませんが、「たとえ無数の衝突を経ても、粒子たちの振る舞いは統計的な平均像から大きく逸れない」ことを保証したと言えばイメージしやすいでしょう。
こうして任意の長時間スケールでニュートン力学からボルツマン方程式を導けるという、大きな一歩が達成されたのです。
中間からマクロ(ボルツマン方程式 → 流体力学方程式)
次に研究チームは、得られたボルツマン方程式から従来の流体力学の方程式(マクロの方程式)を導くことに取り組みました。
この部分は物理学・数学の分野では「流体力学極限」として知られ、過去の研究で多くの成果が蓄積されています。
気体分子の平均自由行程(衝突と衝突の間の距離)がゼロに近づく、つまり衝突頻度が極めて高くなる極限では、粒子の集団は滑らかな流体のように振る舞います。
このときボルツマン方程式から導かれるのが、オイラー方程式やナビエ–ストークス方程式といった流体の方程式です。
Deng氏らはこの極限操作を厳密に行い、2種類の基本的な流体方程式をニュートン力学から導出することに成功しました。
一つはインクームプレッシブル・ナビエ–ストークス–フーリエ方程式と呼ばれるもので、粘性のある流体(空気や水など)の流れと熱の伝わりを記述する式です。
もう一つは圧縮性オイラー方程式で、粘性を無視できる流体(例えば音波や衝撃波のような気体の運動)を記述します。
これらはいずれも工学や自然現象の解析に日常的に使われている基本方程式です。
以上の二段階を組み合わせることで、研究チームはニュートンの粒子論から連続体の流体方程式までを一直線に結ぶことに成功しました。
言い換えれば、「微視的な世界の法則から巨視的な世界の法則を導けることを示した」ことになります。
これはヒルベルトが19世紀末に夢見た課題を正面から射抜いた、歴史的偉業と言えるでしょう。
理論の土台が固まると、空も海も計算しやすくなる

今回の成果は、流体力学の方程式そのものの形を変えるものではありません。
エンジニアや物理学者が使うオイラー方程式やナビエ–ストークス方程式が突然アップデートされるわけでもありません。
しかし、この理論の裏付けが与える影響は計り知れないものがあります。
まず第一に、私たちがこれまで経験的に正しいと信じて使ってきた流体の方程式が、もっと根本的な原理(ニュートンの運動法則)から必然的に導かれることが示されました。
これは「なぜその方程式でうまくいくのか」を深いレベルで理解できたことを意味します。
今回の証明により、ニュートン力学・ボルツマン方程式・オイラー/ナビエ–ストークス方程式という三つの理論が矛盾なく一つの現実を記述していることが数学的に保証されたのです。
理論と現実の間に横たわっていた溝が埋められたことで、今後は流体の方程式に対する信頼性が一段と高まり、「なぜそれが成り立つのか」という疑問に対しても明確な答えが得られたと言えます。
さらに、この成果は物理学の他分野にも波及効果をもたらす可能性があります。
例えばプラズマ物理や凝縮系物理、あるいは量子力学や統計力学の領域でも、ミクロな描像(微視的法則)とマクロな描像(巨視的法則)を結びつけようとする研究が数多くあります。
ミクロとマクロをつなぐ数学的なリンクが明確になれば、理論間の食い違いによる予想外の破綻を防ぐことができるだけでなく、新たな現象予測につながる可能性もあります。
実際、「粒子から流体へ」のブレイクスルーは他の難問にもヒントを与えるでしょう。
1900年にヒルベルトが掲げた壮大な夢(物理学の公理化)は非常に広範なものですが、その一角が今回崩れたことで「奇跡の年」と称賛する声も上がっています。
ある数学者グループはSNS上で「彼らは100年越しの問題を解決し、狭い意味でヒルベルト第6問題を完遂した」とまで評しています。
もしこの証明に間違いがないことが確認されれば、それは物理学と数学の歴史に残る一里塚となるでしょう。
そしてこの新たなアプローチによって、今後ほかの未解決問題にも次々と光が当てられていくことが期待されます。
元論文
Hilbert’s sixth problem: derivation of fluid equations via Boltzmann’s kinetic theory
https://doi.org/10.48550/arXiv.2503.01800
ライター
川勝康弘: ナゾロジー副編集長。
大学で研究生活を送ること10年と少し。
小説家としての活動履歴あり。
専門は生物学ですが、量子力学・社会学・医学・薬学なども担当します。
日々の記事作成は可能な限り、一次資料たる論文を元にするよう心がけています。
夢は最新科学をまとめて小学生用に本にすること。
編集者
ナゾロジー 編集部
Views: 0