はじめに
改めて3DCGのレンダラを作りたくなってきたので、自分なりに必要な知識を何回かに分けてメモします。
個人的なメモなのでなにか間違ってるかもしれません。
間違っているところや補足があれば教えていただけると嬉しいです。
初回のこの記事では特に物理ベースレンダリングで必要になる物理量と単位、そして測光量との関係やライトの単位の使い方についてまとめます。
物理量と単位
レンダリングでよく出てくる物理量と単位をまとめます。
| 名前(英語) | 名前(日本語) | よく使う記号 | 単位 |
|---|---|---|---|
| Radiant energy | 放射エネルギー | ||
| Radiant flux | 放射束 | ||
| Radiant intensity | 放射強度 | ||
| Radiance | 放射輝度 | ||
| Irradiance | 放射照度 | ||
| Radiant exitance | 放射発散度 |
放射エネルギー(Radiant energy) [\mathrm{J} ]
放射エネルギー は、ある時間に放射されたエネルギーです。
単位は ジュール(
これ自体は単位としてはレンダリングではあまり直接使わない単位な気もします。
後述の放射束などの単位時間あたりのエネルギーを使うことが多いです。
放射束(Radiant flux) [\mathrm{W} ]
放射束 は、単位時間あたりに放射されるエネルギーです。
単位は ワット(
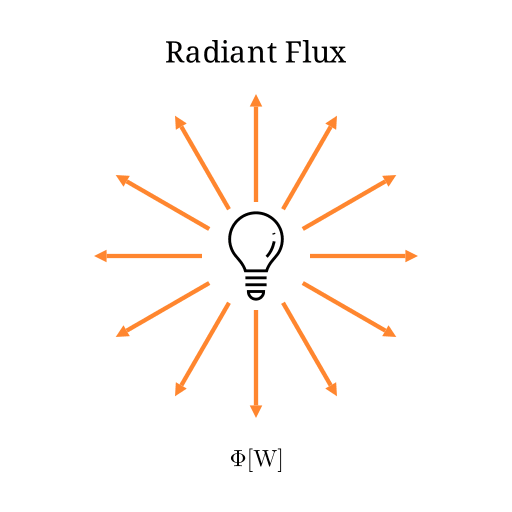
例えば点光源の明るさを
このWは電球の消費電力のW数とは異なります。電球の消費電力は大部分は熱に変わったり、あるいは可視光以外の電磁波のエネルギーとなったりするので、白熱電球が光として放射するエネルギーは10%程度だそうです。
放射強度(Radiant intensity) [\mathrm{W \cdot sr^{-1}} ]
放射強度 は、単位立体角あたりの放射束です。
単位は ワット毎立体角(
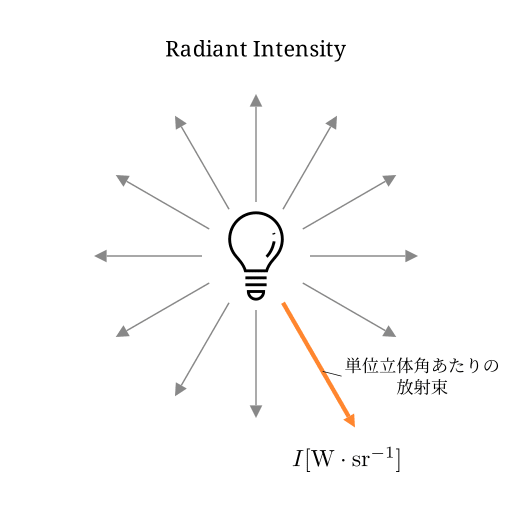
この単位はレンダラーを作るうえでは後述の放射輝度と放射照度ほど目にするわけではないですが、時々出てくる単位です。
単位立体角あたりの放射束ということで放射束に対して立体角での微分値になるので、イメージとしては放射束の特定方向の成分みたいなものでしょうか。
放射輝度(Radiance) [\mathrm{W \cdot sr^{-1} \cdot m^{-2}} ]
放射輝度 は、単位射影面積あたりかつ単位立体角あたりの放射束です。
単位は ワット毎立体角毎平方メートル(
光源の発光を表す際は光源面上の特定の点から特定の方向へ放射される光の強さを表すのに使います。
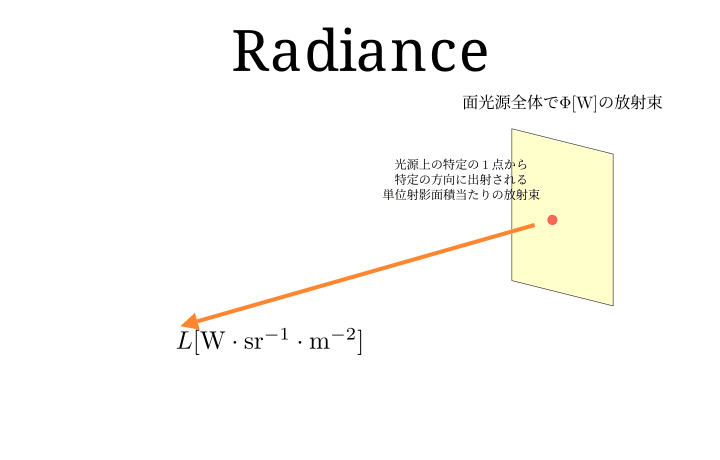
物体表面に届いた光を表す際は、物体表面上の特定の点に特定の方向から入射した光の強さを表すことになります。

これは放射束に対して面積での微分値なので面の上の特定の位置についての値となります。また、立体角あたりの微分値で、さらに射影面積当たりなので、特定の方向の放射束成分にさらに入射ベクトルと法線ベクトルの内積のコサイン項を割ったものになります。
オフラインレンダリングのモンテカルロレンダリングで中心的に登場する単位になります。
単位射影面積あたりというのは、照射する面と光の方向の角度によって値が変わらないようにするための工夫 です。法線方向と入射方向のなす角のコサインで割ることで、面の向きに依存しない物理量となります。
というのも、ある面に斜めから光が入ってくる場合、その分単位面積あたりの光のエネルギー量は減ってしまいます。
次の図のように、上の方から降り注いだときに比べて斜めから降り注いだときのほうが同じ面上の面積当たりの光の太さが小さくなりエネルギー量が小さくなっているのがわかると思います。
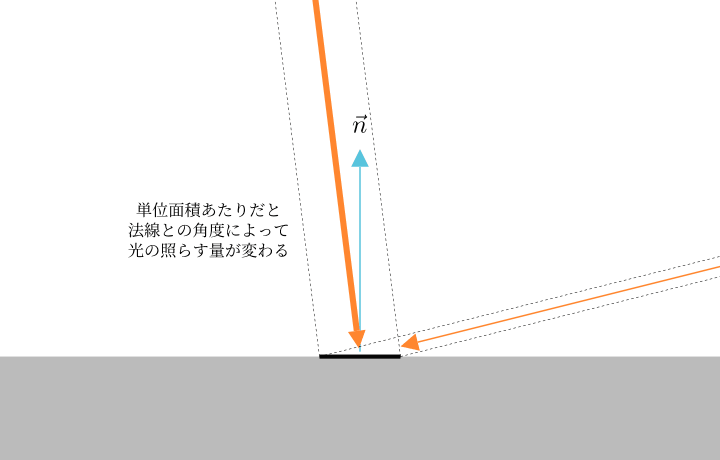
そこで単位面積あたりではなく、斜めの射影面積当たりとすることで、値が正規化されて面と入射ベクトルの角度によって変わらない値となります。
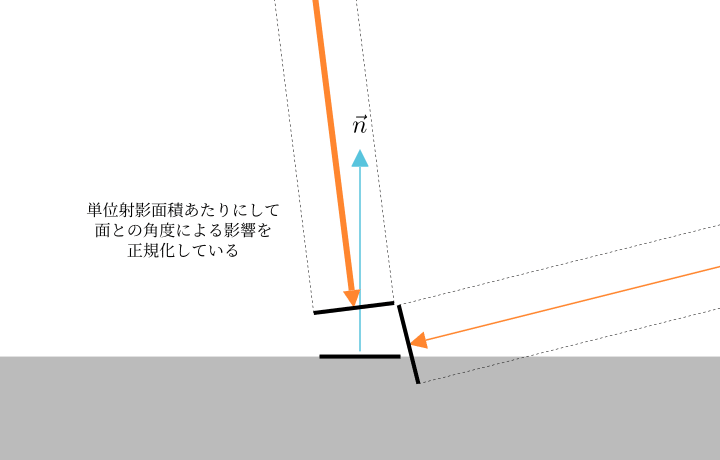
面の向きに依存しない量なので、レイトレでレンダリングする際にある点にある方向から入ってくる光の放射輝度を、次の点から出てきた光の放射輝度をそのまま使って計算できたりと便利に扱えます。
放射照度(Irradiance) [\mathrm{W \cdot m^{-2}} ]
放射照度 は、単位面積あたりの出射される放射束です。
単位は ワット毎平方メートル(
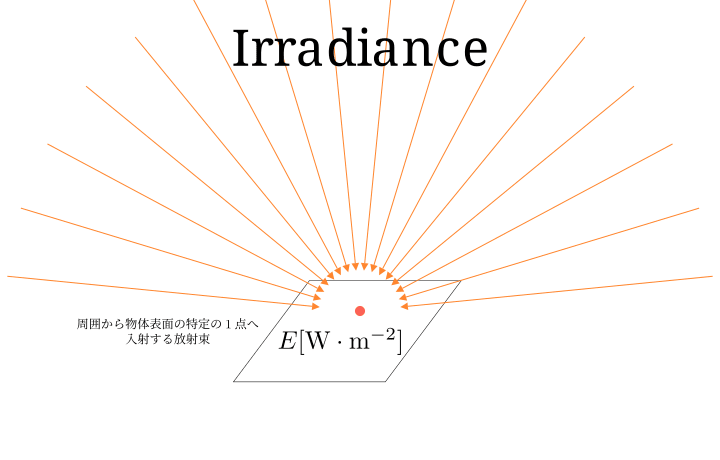
これは放射束の面積についての微分値なので、面の上の特定の位置での入射した光と言ったところでしょうか。
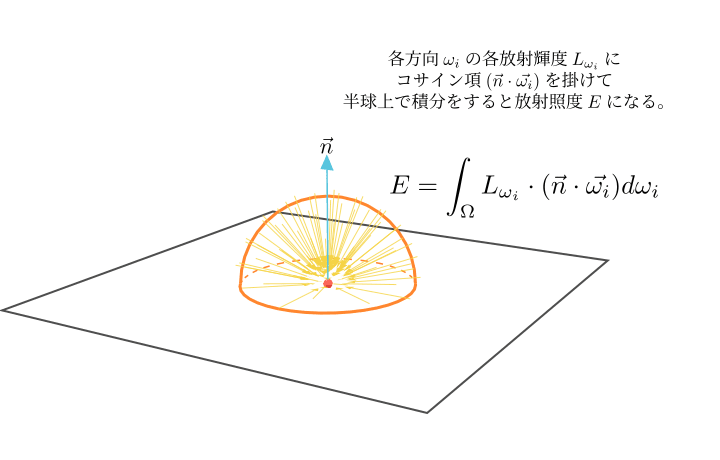
照らされている面の特定の点について、その法線ベクトルが向いている半球全体から入射する放射輝度に、コサイン項を掛けて半球上で積分をすると放射照度になります。 放射照度は放射輝度とは異なり、単位面積あたりの値であって単位射影面積あたりの値ではないため、積分する際にコサイン項を掛けて斜めから入ってきた放射輝度はその分割り引いたうえで積分を計算してやる必要があります。このコサイン項は、斜めから入射する光が単位面積あたりに与えるエネルギーが減少することを表しています。
また、Φ[W]の放射束の点光源からr[m]離れた位置にある点光源を向いた面の放射照度E[
E = \frac{\Phi}{4 \pi r^2}
これは点からr[m]離れた位置にある面の面積は球の表面積の
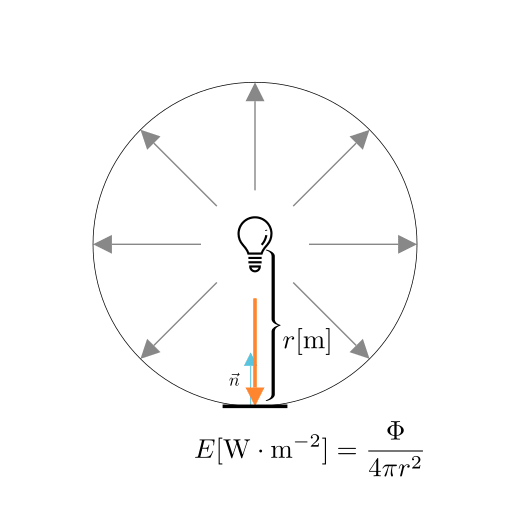
点光源から放たれた光は距離の二乗に反比例して減衰する事がわかります。
放射発散度(Radiant exitance) [\mathrm{W \cdot m^{-2}} ]
放射発散度 は、単位面積あたりの射出される放射束です。
単位は ワット毎平方メートル(
放射照度が外から照らされるときに使うのに対して、こちらは自身が発光したりして外に出ていく光エネルギーを指すときに使うようです。
ただ、放射照度と単位が同じなので放射照度の方を混同して使うこともあるようです。
測光量
物理量は光の電磁波としてのエネルギーでした。
しかし、人間が感じる明るさは必ずしも物理量そのものではありません。
例えば可視光の外の赤外線や紫外線として放射束のエネルギーが放たれていたとしても、人間の目には明るさは感じられません。
人間は光の波長に応じてそのエネルギーに対してどのくらいの反応を感じるかというのが決まっています。この人間が感じる明るさへの反応を図るための単位として、放射量を眼の感度で評価した量である 測光量 という単位があります。
これは人間の感覚である心理量を考慮した値なので、測光量は心理物理量と言われています。
測光量の単位を対応する物理量とまとめると次のようになります。
| 測光量(英語) | 測光量(日本語) | 単位 | 対応する物理量 |
|---|---|---|---|
| Luminous energy | 光度エネルギー | 放射エネルギー | |
| Luminous flux | 光束 | 放射束 | |
| Luminous intensity | 光度 | 放射強度 | |
| Luminance | 輝度 | 放射輝度 | |
| Illuminance | 照度 | 放射照度 | |
| Luminous exitance | 光束発散度 | 放射発散度 |
物理量との変換には波長ごとの 視感度関数(luminous efficiency function)V(λ) と 最大視感効果度(maximum luminous efficacy) が使用されます。
最大視感効果度は人間にとって最も明るく見える波長での放射エネルギーでの値で 683 lm/W となります。これは 波長555 nm(緑色光)単波長のとき のものです。
他の波長でのlmを計算するには 視感度関数V(λ) を使います。
V(λ)は波長ごとの最大視感効果度に対する割合として定義されています。
この
X_v(λ) = 683 × V(λ) × X_e(λ) [\mathrm{lm/W}]
光度エネルギー
光度エネルギー は放射エネルギーに対応する測光量で、単位は ルーメン秒[
光束
光束 は放射束に対応する測光量で、単位は ルーメン[
単色光(555nm)では
身の回りのものだと:
- 一般的な白熱電球(E26口金)
- 40Wで485lm以上
- 60Wで810lm以上
- 100Wで1520lm以上
- 天井のシーリングライト 2700~5600lm
- プロジェクター一般向け 3000~4000lm
- ステージ照明 5000~10000lm
光度
光度 は放射強度に対応する測光量で、単位は カンデラ[
単色光(555nm)では
身の回りのものだと:
- ロウソクが1cd(カンデラの単位の元々の定義の基準)
- 液晶テレビ (一般的)で250~500cd
- スマートフォンの画面で250~450cd
- 懐中電灯(家庭用)で10~500cd
- 自動車のヘッドライトで約25000~40000cd
- 満月の地球から見た光度が約0.25cd
光度(カンデラ)は方向に依存する量であるため、同じ光源でも測定方向によって値が異なります。多くの照明器具では、最も明るい方向(最大光度方向)での値が仕様書に記載されます。
全方位に光を照らすものはルーメンで表現してスポットライトやビームライトのようなものをカンデラで示すことが多いようです。
輝度
輝度 は放射輝度に対応する測光量で、単位は カンデラ毎平方メートル[
単色光(555nm)では
身の回りのものだと:
- 一般的なディスプレイ200~350 nit
- HDRディスプレイで400~1000 nit
- 太陽(正午時)で1600000000 nit
- 青空(晴天時)で3000~5000 nit
- 月の表面(満月時)は約2500 nit
- LED電球の発光面は10000000~50000000 nit
- 裸の白熱電球フィラメントで7000000 nit
- 蛍光灯の表面は12000nit
- 月の表面(満月時)は約2500 nit
人間が不快グレアを感じる閾値は概ね10000 nitで、人間が認識できる最小輝度(完全暗順応時)が約0.000001 nitと言われています。
照度
照度 は放射照度に対応する測光量で、単位は ルクス[
単色光(555nm)では
身の回りの環境だと:
- 自然光
- 直射日光(夏の晴れた日)は100000~150000 lx
- 直射日光(冬の晴れた日)は35000~65000 lx
- 曇り空の日中は5000~32000 lx
- 日陰(晴天時)は10000~25000 lx
- 夕暮れ(日没直前)は50~500 lx
- 満月の夜(晴天時)は0.2~0.5 lx
- 星明かりのみ(新月時)は0.001~0.002 lx
- 一般的な住宅
- 全般照明で50~75 lx
- 団らん・娯楽で150~300 lx
- キッチン(調理台・流し台)で200~500 lx
- 寝室で10~30 lx
- 読書に適した照明で500~750 lx
- JIS(日本工業規格)の推奨照度
- 超精密作業は1500~3000 lx
- 精密作業は750~1500 lx
- 普通作業は300~750 lx
- 粗い作業は150~300 lx
- 視作業をほとんど必要としない場所は75~150 lx
光束発散度
光束発散度 は放射発散度に対応する測光量で、単位は ルクス[
こちらも単色光(555nm)では
人間の明るさの知覚について
測光量は人間の知覚に基づいた心理物理量です。
しかし、人間が実際に感じる明るさは測光量よりも複雑なようです。
例えば次のような事情で、人間は物理量に比例しない明るさの認識をします。
- ウェーバー・フェヒナーの法則やスティーブンスの法則
- 物理的な刺激の強さと主観的な明るさの感じ方は非線形である
- 明暗順応
- 周囲の明るさによって同じ物理的な刺激でも知覚する明るさは変わる
- 対比効果
- 周囲との相対的な関係で明るさの感じ方が変わる特性
物理量を扱う物理ベースレンダラーでは直接この人間の認知での明るさを扱うことはないですが、映像を表示する場合やゲームなどでレンダリングした結果を画面に表示する場合に、人間の知覚を考慮した処理が必要になる場合があります。
例えばゲームをHDRモニターで遊ぶ際にで明るさのキャリブレーションを行ったりしたことがあるかもしれません。ゲームのHDRモニターのキャリブレーションではモニターの出力できる最大と最小の値を黒い模様が見えなくなる位置と白い模様が見えなくなる位置で決めた後に、例えば18%グレーだとか代表的なシーンなどの見え方をちょうどよく調節してもらうことがあります。
人間の知覚する明るさは、たとえモニターから同じ明るさの物理量の光を放出したとしても、モニターの置いてある部屋の周囲の明るさなどによって変わってきてしまうため個別にプレイヤーがキャリブレーションを行う必要があるわけです。
ちなみに18%グレーは写真撮影やデジタルイメージングにおいて重要な基準となる濃度のグレーで、入射光の18%を反射する中間調のグレーのことを指します。人間の知覚が対数的であることをもとに0%から100%の間で18%が人間の知覚に対してちょうど中間的な50%の明るさとなります。
HDRモニターにレンダリング結果を表示する際に考慮することは他にも色域やトーンカーブの扱いなどなどがあり、ここでまとめるには量が多いので、また別の記事でHDRモニターにレンダリング結果を表示する際に必要なことをまとめた記事を作ろうと思います。
「単位立体角あたり」とは何か
物理量や測光量のいくつかの単位に 「単位立体角あたり」 というのが出てきました。
私はCGを学び始めた当初、この「単位立体角あたり」というのを飲み込むのに時間がかかったので、特別にメモを書いておきます。
立体角[\mathrm{sr} ]
まずは立体角について説明します。
立体角 は、3次元上の角度のことです。
二次元での角度がラジアンとして弧度法で単位円上の長さとして定義したように、立体的な角度は 単位球上に占める面積 として定義されます。
単位は ステラジアン[
単位球全体で球の表面積は
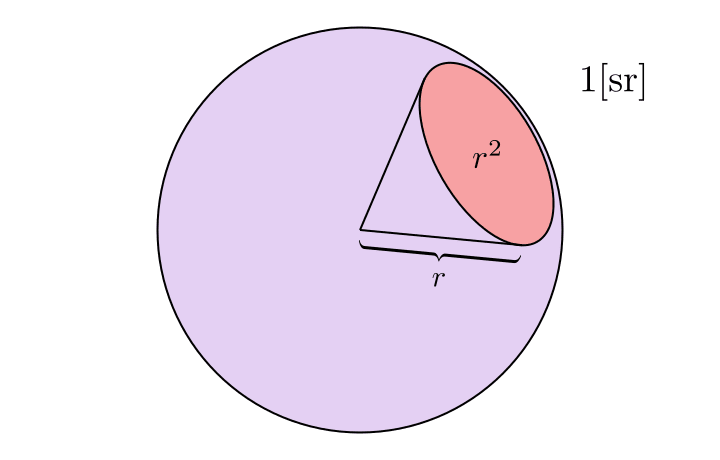
単位立体角あたりの誤った理解
単位立体角あたりというのは1srあたりの量ということになりますが、1srあたりと言われると上図の1srの範囲にわたって値が分布しているようなイメージをもってしまうかもしれません。
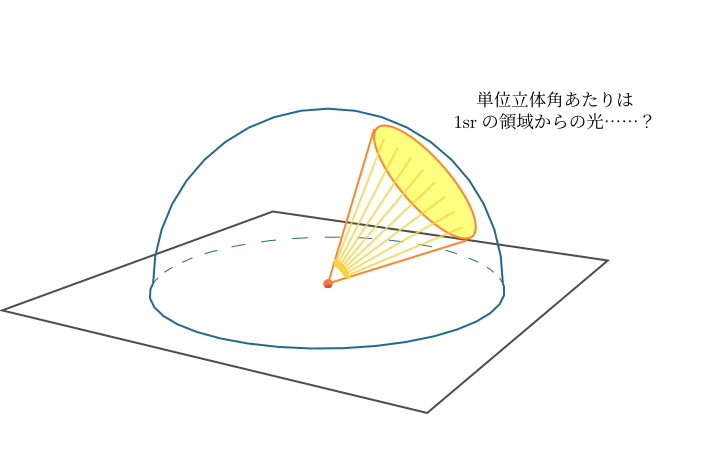
しかしこれは間違ったイメージです!
単位立体角あたりの量というのは、ある領域にわたって分布した量の和とかではなく、あくまで特定の方向に対する値 になります。
なぜ「単位立体角あたり」とすると特定の方向に対する値になるのかを、この後で説明していきます。
単位立体角あたりと微分と積分の関係
単位立体角あたりというのは、ある量を 立体角で微分した微分値 になります。
逆にこの単位立体角あたりの量を全天球の立体角で積分すると全体の量が出てきます。
例えば放射強度は放射束を立体角で微分したものです。
放射強度を全方向について積分すると放射束になります。
速度と距離の関係を思い浮かべてみる
微分と積分の関係で一番馴染み深くわかりやすいのは速度と距離の関係です。
そこで、速度と距離の関係について復習して、その類推で単位立体角あたりの理解を深めてみましょう。
復習ですが 速度とは「単位時間あたりの移動距離」 のことになります。
単位としては メートル毎秒[m/s] でしたね。
ここである時間における速度の変化が次のグラフのようだったとします。
横軸が時間軸で縦軸が速度です。
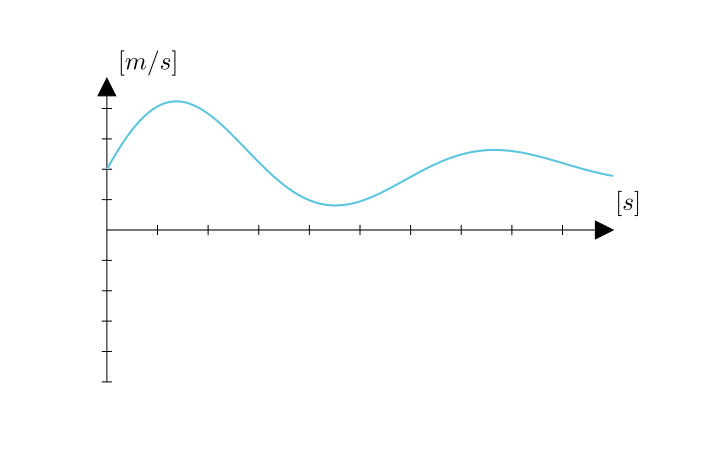
このとき時刻aからbまでの間の移動距離は、区間[a, b]で積分した面積として表すことができます。
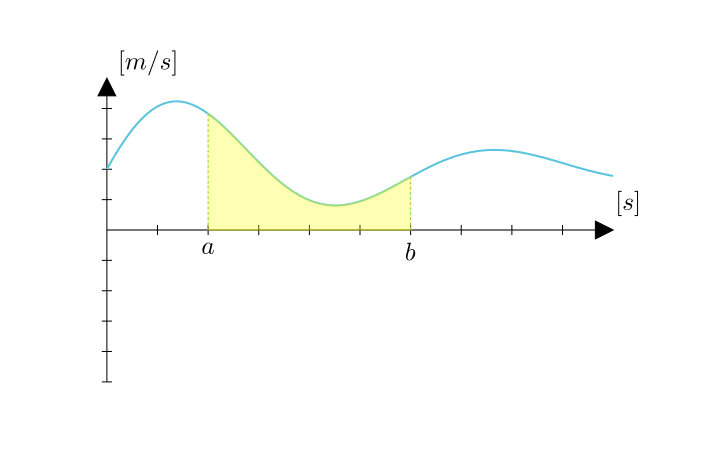
そして重要なことですが、このときの ある時刻tの速度v[m/s] は、その時刻の一瞬の値 です。
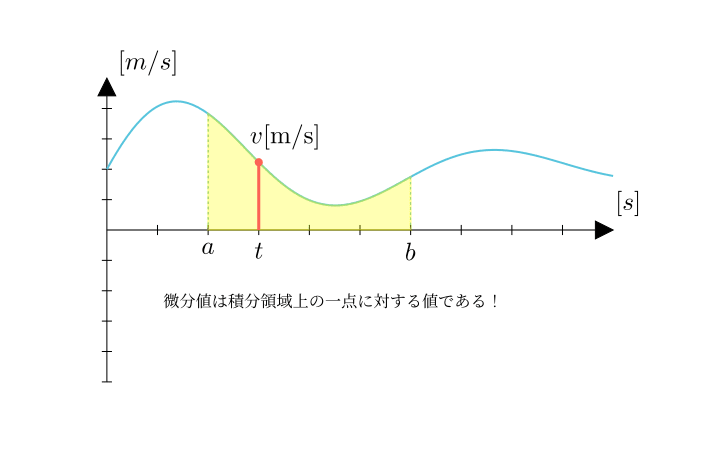
速度の定義が単位時間あたりの距離だからといって、 速度は1秒間持続した領域の面積を表すわけではありません。 あくまでこの速度で1秒間移動したとしたら、そのくらいの距離になるというだけで、速度自体はその瞬間瞬間での値です。
「単位時間あたりの距離」というのは積分のドメインである時間について、微分値としてドメイン上の点である「ある瞬間の時刻」での値であって、時間の範囲を持ったものではありません。
単位立体角あたりの正しい理解
「単位時間あたりの距離」である速度が、積分のドメインの時間に対して領域を持っているのではなく、あくまで微分値として時間の点の一瞬の時刻での値だったことの類推から、「立体角あたり」についての理解を考えてみましょう。
「立体角あたり」というのは積分のドメインは立体角の球上になります。
「立体角あたり」という単位の値は、その球の領域ではなく微分値として 単位球上の一点での値、つまり 特定の方向一点に対する値ということになります。
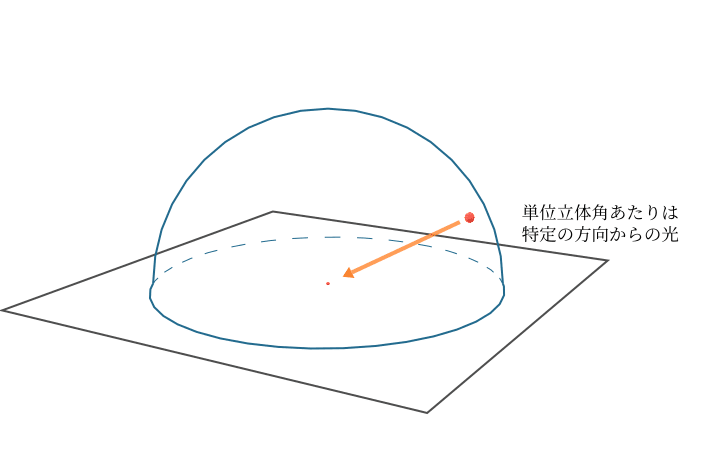
この値で均一に1srの領域を占めたとき、その領域を積分するとその値になる、ということではありますが、「立体角あたり」の単位の値そのものについては領域に定義される値ではなく特定の方向に定義される値であることがわかると思います。
これが「単位立体角あたり」な単位が方向を持った単位である理由です。
放射強度や放射輝度は「単位立体角あたり」の単位を持った量なので、特定の方向に対する値になります。
よく使われるライトの単位
物理ベースレンダラーではライトに物理的な単位を割り当てることになります。
その際に物理ベースレンダラーでライトの種類ごとによく使われる単位をまとめます。
点光源
点光源はWかlmなどの放射束もしくは光束の単位を使うことが多いです。
このエネルギーが距離によって減衰していくことになります。
平行光源
平行光源は
このとき、直接法線照度(Direct Normal Illuminance)という法線に対して垂直に照らしたときの明るさで指定することが多いです。
面光源
面光源では
面光源上の点の明るさを直接指定していることになります。
スポットライトの扱い
スポットライトは扱いが少しややこしいです。
スポットライトのコーンアングルの内側にすべての光のエネルギーが注ぐとした場合、光源の明るさを点光源と同じWやlmで指定していると、コーンアングルを変えることで照射した面の明るさが変わることになります。
しかし、シーンのスポットライトのコーンの大きさを変える際に、照明の明るさ自体が変わるのはシーンの調整がしにくくなったりします。
そこで、照明に指定したWやlmがすべてコーンアングルに注ぐわけではないとすることがあります。
例えば、スポットライトは点光源をマスクしたような光源として扱うことがあるようです。
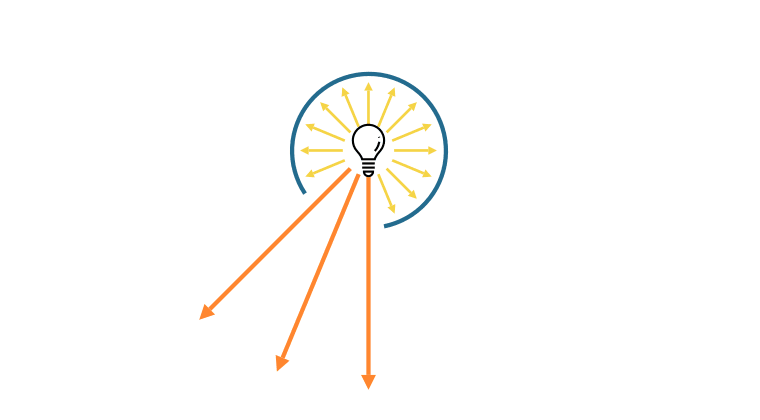
これでスポットライトを点光源と同じWやlmで指定しても、コーンアングルを変えても明るさが変わらないようにすることができます。
ゲームエンジンのFrostbiteなどはPunctual Lightはlmで指定しコーンアングルでは明るさが変わらないようにしているため、この方法でスポットライトの明るさを扱っていることになります。
この方法の場合、指定したW数全部がシーンを照らすために使われていないことには注意が必要です。
一方でUnrealEngineでは スポットライトと点光源の両方でcdの放射強度や光度を使って指定できる ようです。
スポットライトの指定としてはコーンアングルによらず特定の方向の明かりを指示できるため、cdの方が適しているというのはそのとおりですね。
そしてUnrealEngineでは、スポットライトと点光源で同じ値を指定したら同じ明るさになったほうがわかりやすいということもあり、このスポットライトをcdで表すのに合わせて 点光源もcdで表せる ようです。
点光源は全方向に均等に放射強度を発していると考えれば、このcdからlmに変換するのは立体角で全天球で積分するので
点光源とスポットライトで同じ単位を使えるようにするために、点光源の方にスポットライトを合わせるかスポットライトの方に点光源を合わせるかはエンジンなどによって違いますが、おおよそこのような感じで扱われているようです。
Punctual Lightと放射輝度の話
レイトレでは基本的に放射輝度をたどることになります。
しかし上述のように 光源の種類によっていろいろな単位を使うのは何故でしょうか。
すべて放射輝度[
しかし、これには理由があります。
ある面光源がΦ[W]の放射束を持っているとします。
このときこの光源からある点に向かって届く放射輝度たちを考えましょう。
光源上の各点からそれぞれの方向からの放射輝度を考えられることになります。
各方向の放射輝度をこの面光源が単位球に投影された面積で(距離の逆二乗も考えたうえで)積分すると結果がΦになることになります。
このとき、放射輝度の明るさは面光源の面積の大きさに応じて変化します。
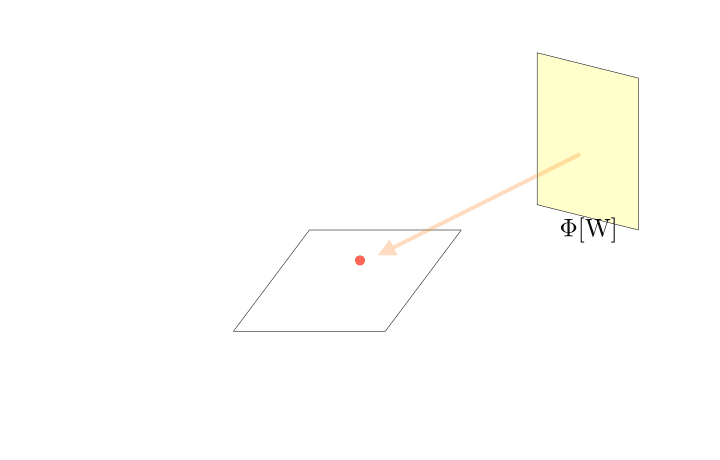
面光源の面積が大きくなると、光源全体が同じ放射束Φ[W]でも、放射輝度は小さくなります。
面光源の面積が小さくなると、光源全体が同じ放射束Φ[W]でも、放射輝度は大きくなります。


点光源というのはこの面光源の面積が0になったものです。
面積をゼロに近づけていくと、その分投影面積が小さくなり、放射輝度としては大きな値を取るようになります。
最終的に面積をゼロにすると点光源の放射輝度は無限大になるようなデルタ関数的な扱いをしなければならなくなります。 デルタ関数は超関数と呼ばれるもので普通の関数とは性質が違うもので取り扱いが面倒なものです。
平行光源も同様に大きさがゼロとなる光源になります。
このように点光源や平行光源は放射輝度を考えようとすると、デルタ関数的な扱いをせざるを得ず、また値は無限大のような値になるため、放射輝度の値を直接指定して明るさを指定するというのは不可能です。このような理由から、点光源や平行光源は放射輝度を使うのではなく、放射束や放射照度を指定することになります。
これらの光源でもレンダリング方程式の立体角の積分の外に出して計算してやれば、放射輝度を求めずとも計算を完結させることが出来ます。
BRDFは放射輝度と放射照度の比です。
点光源だけからある点を照らす放射照度は、
平行光源はもっと単純に距離の逆二乗を考えずにそのまま放射照度を使うことが出来ます。
リアルタイムレンダリングでは立体角での積分をモンテカルロ法で計算する手間がないので、こちらの点光源や平行光源の計算を使うことが多いですね。
点光源や平行光源のような面積の大きさがゼロの光源のことをPunctual Lightと呼んだりします。ここでのPunctualは「時間を守る」「几帳面な」ではなく幾何学の「点」の方の意味でしょう。
Punctual Lightの理論的な扱いはkinankomotiさんの記事の解説が良かったので、記事をおすすめしておきます。
ライトの単位を選べるレンダラー
レンダラーによってはライトの単位を選んで指定できるものがあります。
例えばVRayというレンダラーではVRayLightRectで単位を次から選べます。
- default
- Lumens
- lm/m/m/sr
- Watts
- w/m/m/sr
この場合も内部的には放射輝度に揃えて計算されていると思いますが、単位の指定によってライトの挙動が変わります。
Wで指定する場合、光源全体が出力する光の量ということになります。
この場合、長方形ライトの面積が大きくなってもシーン全体に放出する光の量は変わらないです。しかし、長方形ライトの各点の明るさは面積を大きくすると引き伸ばされて明るさが小さくなります。
W/m/m/srで指定する場合、光源の各点の明るさを指定するものになります。
そのため長方形ライトの大きさを変えても各点の明るさは変わらないです。
そのかわり、長方形ライトの面積が大きくなるとシーンに放出する光の量は大きくなることになります。
光源上の各点の明るさを変えたくない場合と、光源がシーンに与える明るさの総量を変えずにハイライトなどの形を変えたい場合とで使う単位を切り替えたりできるかもしれません。
参考にしたサイト・書籍
基本的な放射量と単位についてはPhysically Based Rendering: From Theory to Implementation 4th Editionを参考にまとめました。とくにChapter 4: Radiometry, Spectra, and Colorが参考になります。
また、放射量や測光量についてReal-Time Rendering, 4th Editionも参考になりました。とくにChapter 8: 光と色が参考になります。
日本語だとemadurandalさんの物理ベースレンダリングを柔らかく説明してみる(5)の記事も大変わかりやすく参考になりました。この「物理ベースレンダリングを柔らかく説明してみる」シリーズの記事は大変おすすめです。
測光量と視感度関数については産総研のページなどが参考になります。
また、色や光の心理的な側面については色彩検定の教科書も参考になりました。
よく使われるライトの単位についてはUnreal Engineのドキュメント、Frostbiteの技術ペーパー、Godotのドキュメントなどのゲームエンジンのドキュメントが参考になります。
また、商用レンダラーのドキュメントも参考になります。今回は特にVRayのドキュメントが使える単位などについて詳しく乗っていたので取り上げています。
おわりに
この記事では、光の物理量や測光量や心理測光量、ライトの単位についてまとめてきました。
物理ベースレンダラを書くには、これらの単位の扱いを意識してプログラムを書く必要があります。いわばレンダラを書くうえでの基礎知識なので、改めてメモをまとめることで復習できてよかったです。
次の記事では積分をするときの変数変換とヤコビアンの話、それから立体角での積分が何者なのかについて簡単にメモを書こうと考えています。まだ書いていないので、次回はいつになるかわかりませんし、気が変わるかもしれません。
Views: 0

