2つの物質を反応させるとき、反応速度は一般的に2つの物質の濃度の関数になる。一方で化学平衡では、順反応と逆反応が同時に起こっていると考える。そこで、今回は化学平衡反応が生じている際にどのように反応物や生成物の濃度が変化するのかを計算機を用いた数値計算を用いて調査する。具体的には、反応速度論の概念から化学平衡の式を導出し、両者が等価であることをPythonを用いて視界的に理解することを目指す。
以下、2つの反応について考察する。
\ce{A + B [k_1][k_2] AB }
\ce{A + 2B [k_1][k_2] AB_2 }
この2つの式の違いは、$A$と$B$が結合する原子数の差である。これが、反応速度や平衡条件にどのような影響を与えるのかを調査する。
濃度の1乗に反応速度が比例する場合
反応の過渡応答
以下のような化学反応式を考える。
\ce{A + B [k_1][k_2] AB }
このときの化学反応速度は、以下のように表される。
\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{d[A]}{dt}=k_2[AB_2]-k_1[A][B] \\
& \frac{d[B]}{dt}=k_2[AB_2]-k_1[A][B]\\
& \frac{d[AB]}{dt}=-(k_2[AB_2]-k_1[A][B])
\end{aligned}
\right.
\end{equation}
ここで、区分求積法より以下の式が近似的に成立する。
\begin{equation}
\left\{ \,
\begin{aligned}
& [A]_{t=t+dt}=[A]_{t=t}+\frac{d[A]_{t=t}}{dt}dt \\
& [B]_{t=t+dt}=[B]_{t=t}+\frac{d[B]_{t=t}}{dt}dt \\
& [AB]_{t=t+dt}=[AB]_{t=t}+\frac{d[AB]_{t=t}}{dt}dt
\end{aligned}
\right.
\end{equation}
平衡状態
一方で、初期状態から平衡状態に移動するとき、$[AB]$の濃度が$x$だけ変化したとする。このとき、平衡状態の濃度は以下のようになる。
\begin{equation}
\left\{ \,
\begin{aligned}
& [A]=[A]_0-x \\
& [B]=[B]_0-x\\
& [AB]=[AB]_0+x
\end{aligned}
\right.
\end{equation}
したがって、その時の順反応と逆反応は平衡するので、
k_1[A][B]-k_2[AB]=k_1([A]_0-x)([B]_0-x)-k_2 ([AB]_0+x)=0
が成立する。今回は、この$x$に関する方程式を2分法で解く。
ただし、2分法については。以下の記事を参照されたい。
プログラム
さて、上記の考察をもとにして以下のようなプログラム(反応の過渡応答と平衡時の濃度を推定するログラム)を作成した。
ただし、2分法の上限と下限の値については経験則を採用した。
python chem_v1.py
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#反応速度定数
k1=1
k2=1
#反応式: A + B ⇌ AB
#反応速度: v = k1 * A * B - k2 * AB
#反応物の濃度
A_ary=[]
B_ary=[]
AB_ary=[]
n=100
#微小時間
delta_t=0.01
#反応物の初期濃度
A0=1
B0=2
AB0=0
A = A0
B = B0
AB = AB0
L=0.7
def equation(x):
v_k1=k1*(A0-x)*(B0-x)
v_k2=k2*(AB0+x)
return (v_k1 - v_k2)
#初期値
## 最大値
x_max=max(A0,B0)
## 最小値
x_min=0
#二分法
x=(x_min+x_max)/2
while abs(equation(x))>10**-5:
x=(x_min+x_max)/2
if equation(x)*equation(x_max)0:
x_min=x
else:
x_max=x
#過渡応答
t=0
t_max=1
t_ary=[]
while tt_max:
#反応速度
vA=k2*AB- k1*A*B
vB=vA
vAB=-vA
#反応物の濃度変化
A =A+ vA * delta_t
B =B+ vB * delta_t
AB =AB+ vAB * delta_t
#濃度が負にならないように制限
A = max(A, 0)
B = max(B, 0)
AB = max(AB, 0)
#時間の更新
t += delta_t
#濃度を保存
A_ary.append(A)
B_ary.append(B)
AB_ary.append(AB)
t_ary.append(t)
#濃度の過渡的な変化をプロット
plt.plot(t_ary, A_ary, label='A',color='red')
plt.plot(t_ary, B_ary, label='B',color='blue')
plt.plot(t_ary, AB_ary, label='AB',color='green')
#平衡濃度
plt.plot(t_ary, [A0-x]*len(t_ary), linestyle='--', color='red', label='Aの平衡濃度')
plt.plot(t_ary, [B0-x]*len(t_ary), linestyle='--', color='blue', label='Bの平衡濃度')
plt.plot(t_ary, [AB0+x]*len(t_ary), linestyle='--', color='green', label='ABの平衡濃度')
plt.xlabel('時間 (s)')
plt.ylabel('濃度')
plt.title('反応物の濃度変化')
plt.legend()
plt.savefig("reaction_concentration.png")
plt.show()
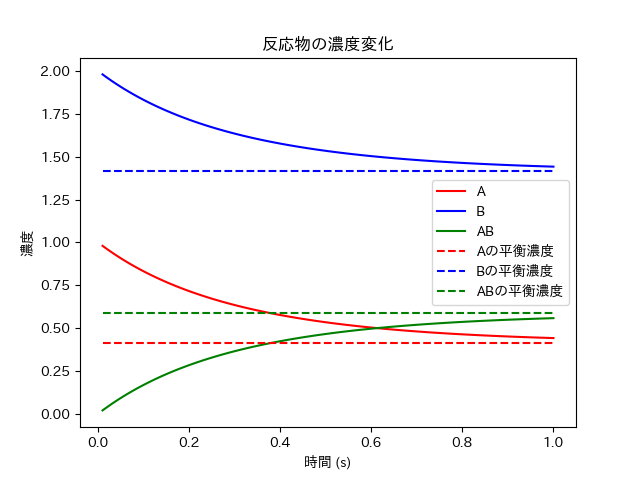
これを実行すると以下のようなグラフが出力される。
このように、時間に対して1次遅れのような反応をする。また、十分に時間が経過したとき、平衡濃度に漸近することもわかる。
濃度の2乗に反応速度が比例する場合
反応の過渡応答
以下のような化学反応式を考える。
\ce{A + 2B [k_1][k_2] AB_2 }
このときの化学反応速度は、以下のように表される。
\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{d[A]}{dt}=k_2[AB_2]-k_1[A][B]^2 \\
& \frac{d[B]}{dt}=2(k_2[AB_2]-k_1[A][B]^2) \\
& \frac{d[C]}{dt}=-(k_2[AB_2]-k_1[A][B]^2)
\end{aligned}
\right.
\end{equation}
ここで、区分求積法より以下の式が近似的に成立する。
\begin{equation}
\left\{ \,
\begin{aligned}
& [A]_{t=t+dt}=[A]_{t=t}+\frac{d[A]_{t=t}}{dt}dt \\
& [B]_{t=t+dt}=[B]_{t=t}+\frac{d[B]_{t=t}}{dt}dt \\
& [C]_{t=t+dt}=[C]_{t=t}+\frac{d[C]_{t=t}}{dt}dt
\end{aligned}
\right.
\end{equation}
平衡状態
一方で、初期状態から平衡状態に移動するとき、$[AB_2]$の濃度が$x$だけ変化したとする。このとき、平衡状態の濃度は以下のようになる。
\begin{equation}
\left\{ \,
\begin{aligned}
& [A]=[A]_0-x \\
& [B]=[B]_0-2x\\
& [AB_2]=[AB_2]_0+x
\end{aligned}
\right.
\end{equation}
ただし、化学反応式の係数に十分注意すること。
したがって、その時の順反応と逆反応は平衡するので、
k_1[A][B]^2-k_2[AB_2]=k_1([A]_0-x)([B]_0-2x)^2-k_2 ([AB_2]_0+x)=0
が成立する。今回は、この$x$に関する方程式を2分法で解く。
ただし、2分法については。以下の記事を参照されたい。
プログラム
さて、上記の考察をもとにして以下のようなプログラム(反応の過渡応答と平衡時の濃度を推定するログラム)を作成した。ただし、2分法の上限と下限の値については経験則を採用した。
python chem_v2.py
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#反応速度定数
k1=1
k2=1
#反応式: A + 2B ⇌ 2AB
#反応速度: v = k1 * A * B**2 - k2 * AB
#反応物の濃度
A_ary=[]
B_ary=[]
AB2_ary=[]
n=100
#微小時間
delta_t=0.01
#反応物の初期濃度
A0=1
B0=2
AB20=0
A = A0
B = B0
AB2 = AB20
L=0.7
def equation(x):
v_k1=k1*(A0-x)*(B0-2*x)**2
v_k2=k2*(AB20+x)
return (v_k1 - v_k2)
#初期値
## 最大値
x_max=max(A0,B0)
## 最小値
x_min=0
#二分法
x=(x_min+x_max)/2
while abs(equation(x))>10**-5:
x=(x_min+x_max)/2
if equation(x)*equation(x_max)0:
x_min=x
else:
x_max=x
t=0
t_max=1
t_ary=[]
while tt_max:
#反応速度
vA=k2*AB2- k1*A*B**2
vB=2*vA
vAB2=-vA
#反応物の濃度変化
A =A+ vA * delta_t
B =B+ vB * delta_t
AB2 =AB2+ vAB2 * delta_t
#濃度が負にならないように制限
A = max(A, 0)
B = max(B, 0)
AB2 = max(AB2, 0)
#時間の更新
t += delta_t
#濃度を保存
A_ary.append(A)
B_ary.append(B)
AB2_ary.append(AB2)
t_ary.append(t)
plt.plot(t_ary, A_ary, label='A',color='red')
plt.plot(t_ary, B_ary, label='B',color='blue')
plt.plot(t_ary, AB2_ary, label='AB2',color='green')
plt.plot(t_ary, [A0-x]*len(t_ary), linestyle='--', color='red', label='Aの平衡濃度')
plt.plot(t_ary, [B0-2*x]*len(t_ary), linestyle='--', color='blue', label='Bの平衡濃度')
plt.plot(t_ary, [AB20+x]*len(t_ary), linestyle='--', color='green', label='AB2の平衡濃度')
plt.xlabel('時間 (s)')
plt.ylabel('濃度')
plt.title('反応物の濃度変化')
plt.legend()
plt.savefig("reaction_concentration2.png")
plt.show()
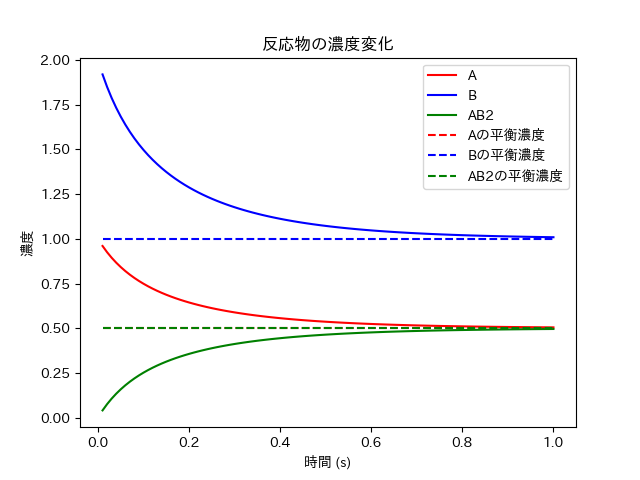
これを実行すると以下のようなグラフが出力される。
このように、比較的変化が大きく濃度の収束も早いことが分かる。
また、当然のことだが、化学平衡の方程式の近似解と反応速度の微分方程式の数値計算の収束値はほぼ一致している。(理論的には厳密に一致するが今回は近似値なので、少し誤差があると考えたがグラフを見るにほとんど無いといえる。)
今回は、高校化学の理論計算で頻出な化学反応速度計算と化学平衡について取り扱った。具体的には、化学平衡の考え方は、化学反応速度計算から始まる。なので、両者によって示唆される平衡条件は一致している必要性がある。そのことを今回はPythonによる計算で確認した。このように、大学以降の化学は数学や物理の考え方を使うことが多い。なので、化学系に進まれる方は、是非とも数学や物理、プログラミングにも多少は興味を持っていただいて勉強することが望ましい。
Views: 0